Сколько в кубе блоков: Сколько керамзитобетонных блоков в 1 кубометре?

Сколько керамических блоков в кубе (1 м3): Поротерм 38, 44, 51

Всех, кто задумывается о строительстве любого объекта из керамических блоков, будь то жилой дом, гараж или любой другой тип постройки, интересует вопрос о том, сколько штук содержится в 1 м3.

Что учитывается при подсчетах

Нужно сказать, что это зависит от нескольких параметров:

• размера блока, который вы намерены использовать;
• типа кладки;
• толщины шва;
• наличия или отсутствия вертикальных швов и других факторов.

Подробнее: Размеры керамических блоков.

В число наиболее популярных марок крупноформатных керамоблоков в России входят Porotherm (Wienerberger), Braer, ТЕРМОБЛОК (Волгоград), ЛСР, Гжель, POROMAX (Краснодарский край), самарский Керакам, а также PORIKAM (Башкортостан) и POROMAX (Славянский кирпич) (Ленинградская область).

Таблица с расчетами

Размеры блоков одного типа у всех производителей – одинаковые или очень близкие. Разница иногда бывает, но она совсем невелика. Так, к примеру, двойной поризованный кирпич (так называемый 2,1НФ) Рязанского завода или ЛСР (Ленинградская область) имеет размеры 250x120x140мм. У Каширского кирпичного завода он ниже на 2 мм (250x120x140мм). Разница не превышает обычные отклонения в геометрии кирпича и практически не влияет на итоговые подсчеты, и вы с достаточной для дальнейших расчетов точностью будете знать, сколько керамических блоков того или иного вида содержится в 1 кубе. Это же касается и более крупных блоков, таких, как Поротерм 38 или 44.    

Наименование	Размеры, мм	Количество, штук в 1м3
2,1 NF	250х120х138	226,2
10,7 NF (блок 38)	380х250х219	45,9
12,4 NF (блок 44)	440х250х219	39,7
14,3 NF (блок 51)	510х250х219	34,2

Расчеты приведены с учетом того, что толщина шва составляет 10мм, а также того, что вертикальных швов для крупноформатных керамических блоков не требуется.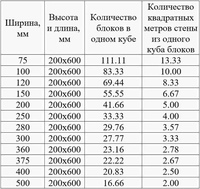 Вместо швов в них задействована система «паз-гребень», которая позволяет обойтись без использования раствора.

Узнайте также: Сколько весят керамические блоки

Таким образом, становится понятным количество керамоблоков в кубе. Опираясь на эти сведения, вы сможете самостоятельно рассчитать и общий объем, который будет необходимо купить. С другой стороны, можно доверить эту задачу профессионалам, которые сделают более детальные подсчеты.

Цена: основные моменты

Цена куба керамических блоков – важный параметр, который закладывается в расчеты при проектировании и строительстве большинства объектов. Указать единую стоимость сложно, поскольку она будет зависеть от множества факторов, в том числе, наименования изделий, а также региона. Так, цена за куб керамоблоков одного и того же производителя (например, Porotherm) в Москве и Санкт-Петербурге будет отличаться, прежде всего, по причине транспортной составляющей.

Сколько пеноблоков в кубе

Когда встает вопрос о строительстве дома, то правильно рассмотреть все возможные варианты строительных материалов, которые можно использовать. Выбор стоит остановить на том, который сможет обеспечить максимальную тепловую изоляцию и сократить расходы на отопление зимой. Также он должен быть достаточно прочным, чтобы прослужить требуемый отрезок времени. Многим приглянулись пеноблоки. Но всегда встает вопрос об их доставке, поэтому важно знать сколько пеноблоков в поддоне. Именно этому, а также нюансам материала посвящена статья.

Чем лучше пеноблок

Строительство из пенобетона известно на протяжении многих лет. Но не каждый может позволить себе сделать монолитные стены из этого материала. Поэтому большей части подходят именно пеноблоки. Их размер значительно превышает габариты стандартного кирпича, поэтому возведение стен происходит быстрее. Положительными сторонами пеноблоков являются:

• меньшая нагрузка на фундамент;
• отличная звукоизоляция;
• хорошая теплоизоляция;
• устойчивость к воздействию влаги;
• продолжительный срок службы;
• устойчивость к открытому огню;
• отсутствие вредных выделений;
• широкие возможности в реализации форм;
• простота обработки;
• простота отделки.

Благодаря небольшому весу пеноблоков из них легко выстроить дом высотой до 5 этажей. При этом понадобиться изготовить дополнительные перемычки, которые увеличат жесткость пеноблоков. Но в сравнении с кирпичом или камнем такое количество пеноблока окажет меньшее давление на фундамент. Пеноблок в своей структуре имеет большое количество замкнутых пузырьков с воздухом. Этим объясняется плохая теплопроводность и отличная звукоизоляция пеноблоков. При этом стенки пузырьков в пеноблоках не имеют пор, что предотвращает проникновение влаги внутрь помещения. Пеноблоки при правильной укладке могут прослужить своему владельцу до 50 лет и больше.

Пенобетон является экологически чистым, т. к. в его состав входит цемент, некоторые добавки и воздух. Не применяется никаких растворителей и других вредных включений, которые бы могли оказать влияние на здоровье человека. Именно поэтому пеноблоки считаются экологически чистыми. Пеноблоки устойчивы к высоким температурам и не горят. Они могут частично обуглиться, но при этом сохранят свою форму для безопасной эвакуации. Материал легко обрабатывается. Чтобы укоротить или располовинить пеноблок, достаточно воспользоваться обычной ножовкой по дереву. При этом срез получится настолько ровным, насколько это вообще возможно. Пенобетон не имеет особых требований к отделке, поэтому многое остается на усмотрение владельца.

Недостатки пеноблока

Человек еще не создал ничего совершенного, поэтому и у пеноблоков есть свои отрицательные стороны:

• усадка;
• пористая структура;
• необходимость армирования;
• хрупкость;
• некоторые расхождения в размерах.

После строительства дома из пеноблока до его отделки придется выждать определенное время. Это связано с тем, что происходит усадка здания. Она может достигать 2% на метр. Пористая структура является огромным плюсом, но внешние пузырьки воздуха не герметичны и в них способна проникать влага, которая при замерзании способна разрушить блок. При укладке пеноблоков потребуется укладка армирующей сетки, которая будет придавать большую жесткость зданию. Она может создать мостики холода. Блоки из пенобетона довольно хрупкие, если их транспортировать неаккуратно или ронять, то они теряют свои свойства. У производителей с небольшим объемом продукции размеры блоков могут разниться. Связано это с качеством выполненных форм. Поэтому приобретать лучше у хорошего поставщика, который способен обеспечить значительные объемы поставок. Видео о производстве пеноблоков можно посмотреть ниже.

Сколько блоков в 1 куб.м

Общепринятые размеры, по которым изготавливают блоки из пенобетона составляют, например, 300×300×600 мм, поэтому будет несложно вычислить, сколько блоков находится в кубе. Есть и другие варианты, которые могут отличаться по ширине и длине. Ниже представлена таблица возможных представителей блоков из пенобетонов.

Чтобы определить, сколько штук блоков поместится в пространство, которое равно 1 кубу, необходимо для начала определить, какой объем занимает один блок. Если брать в расчет размеры, которые приводились выше, то для определения объема необходимо перемножить все указанные величины между собой. В результате получится цифра 0,054 м³. Теперь необходимо найти частное от одного куба и цифры объема блока, которая получилась. Для этого необходимо единицу разделить на 0,054. Результатом будет 18 штук. В автомобиле с объемом кузова в 11,1 кубических метров можно перевести примерно 200 отдельных блоков. Но это при идеальных вычислениях, ведь придется учитывать также высоту паллет, на которые они будут уложены. Ниже приведена таблица, в которой собраны основные возможные размеры блоков из пенобетона и указание количества их содержания в одном кубе.

Сколько блоков на поддоне

Расчет количества блоков, которые содержатся в одном кубическом метре дает идеальное представление о том, сколько могло бы поместиться материала при хранении в определенном помещении. Но размеры поддонов, на которые они обычно укладываются, могут отличаться. Стандартным является размер 80×120 см. Блоки из пенобетона могут укладываться на такой поддон в 3 и 4 ряда. В первом случае при высоте элемента в 300 мм, высота уложенных блоков составит 0,9 метра. При таком значении на поддон можно уложить объем в 0,96 м³. Для размера элемента, о котором говорилось выше, это будет означать 17 штук на поддон. Цифра получилась за счет умножения длины, ширины и высоты, а количество в одном кубе было вычислено умножением 0,96 на уже известную цифру в 18 штук, которая получилась раньше.

Выше на рисунке приведена еще одна разновидность поддона. Его размер составляет 100×120 см. На него можно уложить больше элементов для хранения и транспортировки. Полезная площадь поддона составляет 1,2 квадратных метра. Если уложить на него элементы с высотой в 30 см в три ряда, тогда на него поместиться 19 блоков. Если это сделать в четыре ряда, тогда общая высота составит 1,2 метра, а объем 1,44 м3 (1,2×1,2×1). В таком объеме поместиться 26 элементов с размером 30×30×60 см. Отдельно можно повторить расчеты для блоков с размером в 30×20×60 см. В одном кубическом метре их помещается количество, которое равно 27 целым элементам и еще 0,8 блока. Для того чтобы узнать, сколько их будет на паллетах разных величин, необходимо 27,8 умножить на 0,96 м³. Получиться цифра в 26 целых элементов. Это значение для поддона с размером 80×120 см. На большем поддоне с размером 100×120 см поместится 40 целых блоков. Для блоков из пенобетона с другими размерами можно брать цифры по количеству в объеме, которые приводились выше в таблице и умножать на значение объема при определенной высоте в одном поддоне.

Заключение

Приведенные в статье расчеты, безусловно, понадобятся при закупке материала. Вы сможете самостоятельно высчитать количество, которое можно будет перевести на личном или нанятом транспорте. Учитывая некоторые особенности, вы сможете лучше скомплектовать груз, чтобы не пришлось несколько раз возвращаться в магазин, что понесет дополнительные затраты на топливо.

Расчет количества газосиликатных блоков в 1м3 и в 1м2 | minsk-kirpich.by

1. Главная
/
2. Статьи
/
3. Расчет количества газосиликатных блоков в 1м3 и в 1м2

Сколько в кубе газосиликатных блоков?

 

Если вы решили построить дом или возвести другую постройку из газосиликатных блоков, то, прежде, чем заказать блоки, необходимо подсчитать, сколько необходимо закупить кубов (или штук).

Рассчитать, сколько штук в 1 кубе газосиликатных блоков очень просто.

Количество газосиликатных блоков в кубе зависит от размера самого газосиликатного блока.

Например, для расчёта возьмем газосиликатный блок размером 600 х 300 х 200. Обычно, размеры указаны в миллиметрах, переведем их в метры, таким образом, у нас получиться газосиликатный блок размером 0.6 х 0.3 х 0.2.

Исходя из полученной цифры, рассчитаем объем одного блока. Для этого нам необходимо перемножить высоту на ширину и на длину, т.е. 0.6 х 0.3 х 0.2 = 0.036 м3.

Чтобы узнать количество штук газосиликатных блоков в 1 кубе нам необходимо разделить объем куба (он равен 1 х 1 х 1 = 1) на объем одного блока заданного размера, т. е. 1 / 0.036 = 27.7 штук.  

 

Сколько газосиликатных блоков в 1м2?

 

Чтобы рассчитать, сколько штук газосиликатных блоков определенного размера необходимо в 1м2, нам необходимо, для начала, рассчитать площадь грани газосиликатного блока. В зависимости от того, как будет класться блок, необходимо рассчитать площадь определённой грани. Например, возьмем блок размером 600 х 300 х 200мм (0.6 х 0.3 х 0.2 м).

Площадь граней можно рассчитать, перемножив длину на высоту, в данном случае — 0.6 х 0.3 = 0.18 м2 и 0.6 х 0.2 = 0.12 м2.

Таким образом, делаем расчет количества блоков в 1 м2 – 1 / 0.18 = 5.5 блока, и 1 / 0.12 = 8.3 блока.

Таким образом, рассчитав площадь одной стены (не учитывая дверные и оконные проемы), вы можете легко узнать, сколько вам необходимо купить газосиликатных блоков для постройки с заданными размерами.

При этом, необходимо учитывать не только размер самого блока, но и то, каким образом он будет укладываться.

Если вам нужна помощь в расчете количества блоков или вы хотите купить газосиликатные блоки, вы можете позвонить нам и уточнить любые вопросы.  

В свою очередь, мы предлагаем газосиликатные блоки в Минске различных производителей – Забудова, Минский КСИ и Красносельск. Вы можете выбрать необходимые блоки самостоятельно или позвонить нам для консультации.

Дата публикации: 10.03.2020

Количество скрытых кубиков

Имя: Кэти

Кто спрашивает: Студент
Уровень: Среднее

Вопрос:
Эта проблема заключается в определении количества видимых и скрытых кубов в кубе.

В кубе 3×3 можно увидеть 19 кубиков. 8 скрыты.
В кубе 4×4 можно увидеть 37 кубов. 27 скрыты.
В кубе 5×5 можно увидеть 61 куб. 64 скрыты.
В кубе 6×6 можно увидеть 91 куб. 125 скрыты.

Вопрос:
Объясните, как можно найти количество маленьких кубиков, которые видны и скрыты в кубе любого размера.

Я понятия не имею, как это сделать. Пожалуйста, помогите мне разобраться. Спасибо.

Кэти

Привет Кэти,

Куб трехмерен, поэтому упомянутые вами кубы имеют размер 3x3x3, 4x4x4, 55×5 и 6x6x6.Теперь я вижу, откуда берутся цифры.

Куб 3x3x3 состоит из 27 кубиков, а куб 2x2x2 — из 8 кубиков. 27 — 8 = 19 и, следовательно, числа в первой строке.

В кубе 3x3x3 можно увидеть 19 кубиков. 8 скрыты.

Куб 4x4x4 состоит из 64 кубиков, а куб 3x3x3 — из 27 кубиков. 64 — 27 = 37 и, следовательно, цифры во втором ряду.

В кубе 4x4x4 можно увидеть 37 кубов. 27 скрыты.

В каждой строке АРИФМЕТИЧЕСКИЙ паттерн —

. В кубе nxnxn можно увидеть n ³ — (n-1) ³ кубов.(n-1) ³ скрыты. Чего я не вижу, так это ГЕОМЕТРИИ.

Если у вас есть 27 одинаковых блоков, и вы начинаете строить куб 3x3x3, вы сразу видите, что есть 1 скрытый блок.

Если у вас есть 64 одинаковых блока, и вы начинаете строить куб 4x4x4, вы сразу видите, что есть 8 скрытых блоков.

Если у вас есть n ³ идентичных блоков и вы строите куб nxnxn, то будет (n-2) ³ скрытых блоков.

Ура,
Пол и Пенни Перейти в Центр математики

Безопасность | Стеклянная дверь

Мы получаем подозрительную активность от вас или кого-то, кто пользуется вашей интернет-сетью. Подождите, пока мы убедимся, что вы настоящий человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, напишите нам чтобы сообщить нам, что у вас проблемы.

Nous aider à garder Glassdoor sécurisée

Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet.Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un электронная почта à pour nous informer du désagrément.

Unterstützen Sie uns beim Schutz von Glassdoor

Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem Интернет-Netzwerk angemeldet ist, festgestellt.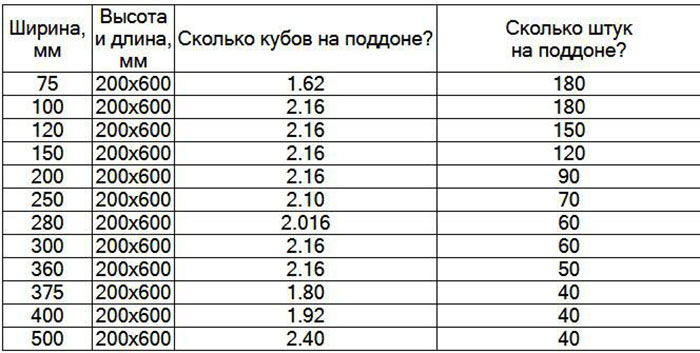 Bitte warten Sie, während wir überprüfen, ob Sie ein Mensch und kein Bot sind.Ihr Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте: .

We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt. Een momentje geduld totdat, мы выяснили, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn. Als u deze melding blijft zien, электронная почта: om ons te laten weten dat uw проблема zich nog steeds voordoet.

Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para informarnos de que tienes problemas.

Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real.Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para hacernos saber que estás teniendo problemas.

Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto confirmamos que Você é Uma Pessoa de Verdade. Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta mensagem, envie um email para пункт нет informar sobre o проблема.

Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet.Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini visualizzare questo messaggio, invia un’e-mail all’indirizzo per informarci del проблема.

Пожалуйста, включите куки и перезагрузите страницу.

Это автоматический процесс.

Ваш браузер в ближайшее время перенаправит вас на запрошенный контент.

Подождите до 5 секунд…

Перенаправление…

Заводское обозначение: CF-102 / 634b927b5a600d3a.

Как построить кубик Сомы

Модули Sonobe следуют правилам традиционного модульного оригами, начиная с плоского квадрата бумаги и затем объединяя части в конструкции без ленты или клея.Куб, который вы можете сделать с этого простого начала, особенно элегантен и привлекателен. Он одинаковый со всех шести сторон и очень стабилен, и его можно комбинировать для создания других конструкций.

Четыре блока Sonobe составляют куб побольше, но зачем на этом останавливаться? Они также образуют строительные блоки так называемого куба Сомы, который был изобретен в начале 1930-х годов Питом Хайном, датским математиком, который изобрел множество других игр и головоломок. ( Говорят, что Хайн придумал эту идею во время лекции по квантовой механике, проведенной физиком Вернером Гейзенбергом, хотя время оспаривается.)

Для создания куба Сомы нужно сложить 27 кубиков Сонобе, а затем объединить их группами по три или четыре на семь частей. Затем части собираются в куб размером три на три на три. Есть 240 способов сложить части вместе, чтобы сформировать куб Сомы — бросьте вызов себе или другу, чтобы найти как можно больше.

1. Сделайте куб Sonobe

Начните с одной страницы газеты и, если необходимо, обрежьте ее до размера 11 на 22 дюйма. Сложите бумагу пополам, затем еще два раза, образуя в общей сложности восемь квадратов 5½ на 5½ дюймов (вам нужно по шесть на каждый куб), и вырежьте их..

1. Возьмите лист бумаги, сложите пополам и разверните. Сложите стороны к центральной складке.

2. Разверните бумагу. Загните верхний правый и нижний левый углы до внешних складок.

3. Загните стороны к центральной складке.

4. Загните правый нижний угол до противоположного края.

5. Заправьте только что сделанный лоскут под левую часть. Загните верхний левый угол к краю и заправьте под правую часть, создав параллелограмм с двумя карманами.

6. Переверните бумагу и загните углы, чтобы получился квадрат, а затем разверните. Сделайте еще пять, чтобы у вас было шесть.

7. Поместите один блок карманами вверх. Затем поместите другой блок перпендикулярно ему и вставьте острие в нижний карман. Поместите другой блок перпендикулярно и вставьте острие в верхний карман, сделав Т-образную форму.

8. Переверните, загните стороны и продолжайте добавлять единицы, заправляя точки в карманы, пока кубик не будет готов.

2. Части куба Сомы

Используйте кубики, чтобы сделать семь фигур Сомы, склеивая их вместе.

3. Решите загадку

Соедините вместе семь фигур сомы, чтобы получился кубик сомы. Есть 240 способов собрать части так, чтобы они образовали куб — вам нужно найти только один (или продолжать).

Лучший друг учителя: блоки Base-10

Учащиеся начальной школы находятся на особой стадии когнитивного развития, когда они начинают переходить от конкретного мышления к абстрактному.Наиболее очевидно это в математике. По мере того, как ваши ученики K-1 переходят в сложение через 10, им нужно будет связать конкретное с абстрактным, чтобы переход был плавным.

Использование блоков с основанием 10 для представления уравнений — отличный способ обеспечить концептуальное понимание этих уравнений и продемонстрировать стратегии их решения. Это позволяет получить гораздо более глубокие знания о сложении, чем просто запоминание фактов. Это более тщательное изучение в сочетании с конкретными моделями приводит к лучшему пониманию и сохранению концепций.

Предполагая, что ваши ученики понимают основы числовой ценности (подробнее по этой теме см. Этот пост), эти стратегии помогут вам обучать сложению до 10 с блоками по основанию 10. На скриншотах ниже показаны реальные онлайн-упражнения, однако вы также можете использовать физические стержни и кубики для реализации этих идей в своем классе.

Все упражнения, упомянутые здесь, являются частью курса HappyNumbers.com и представлены вместе с упражнениями в других представлениях.

1. Сложение и вычитание с помощью 10-стержня

Прежде чем вводить сложение или вычитание через 10, рекомендуется смоделировать несколько задач, в которых используется число 10. Используйте записанные уравнения и проиллюстрируйте их с помощью 10-стержня и дополнительных кубиков.

Добавьте кубики к 10-штанге:

Вычтите 10 из числа, состоящего из 10-стержня и кубиков:

Или вычтите все единицы:

Эти упражнения укрепят понимание ценностей для ваших учеников и являются отличной разминкой перед дальнейшим прогрессом.

2. Отсутствует добавление или вычитание

Как и в предыдущих упражнениях, эти упражнения работают с числами для подростков — комбинацией 10-стержня и кубиков. Однако, вместо того, чтобы складывать их вместе или удалять стержень / кубики, на этот раз студенты меняют логику.

Проблемы с отсутствующими слагаемыми полагаются на понимание десятков и единиц, чтобы определить, сколько еще кубов необходимо:

Проблемы с отсутствием вычитания требуют аналогичного понимания разбиения подросткового числа на десятки и единицы для определения количества, которое было удалено:

3.Плюс / минус без перехода

В качестве следующего шага смоделируйте задачи сложения и вычитания без перехода через 10. Используйте записанное уравнение и смоделируйте числа с помощью стержней и кубов.

Для сложения начните с числа в подростковом возрасте и добавьте кубики (оставаясь в пределах 19):

Для вычитания начните с числа в подростковом возрасте и удалите кубики (не опускаясь ниже 10):

4.

Переход через 10 кубов за раз

Начните переход через 10 с систематического добавления или удаления кубиков один за другим. Момент «ага» наступает, когда ученики должны обменять свои 10 кубиков на жезл:

Или сломайте жезл, обменяв его на 10 кубиков:

5. Решение трех слагаемых путем нахождения 10 первых

В этом упражнении учащиеся учатся воспринимать однозначные числа как части 10.Это подготовит их к будущим стратегиям сложения и вычитания, в которых они разбивают числа на составные части.

Здесь они складывают группы кубиков в определенном порядке, чтобы сначала построить 10, а затем добавить оставшиеся кубики:

6. Разборка

Одна из наиболее эффективных стратегий мысленного сложения, разбиение чисел на части, позволяет учащимся легче добавлять к группе из 10. Здесь они вынуждены заполнять столбец Десятки, выбирая часть дополнения.Затем они перемещают оставшуюся часть в столбец «Единицы». Результат показывает, что они сложили 5 в двух частях, чтобы получить число, состоящее из десяти и двух:

Эта стратегия продолжается по мере того, как учащиеся самостоятельно разбирают дополнение и связывают его с письменным уравнением. По сути, они полагаются на навык из совета №5, чтобы создать проблему с тремя дополнениями. Поэтому они думают о 6 + 5 как о более простом 6 + 4 + 1:

.

7.Почти 10

Наконец, мы рекомендуем обучить стратегии добавления «почти 10». Перемещая один кубик из одного дополнения в другое, ученики учатся визуализировать группу из 10 кубиков и оставшиеся кубики. Опять же, они переводят более сложную задачу сложения (6 + 9) в более простую (5 + 10):

На сайте HappyNumbers.com мы тщательно изучили каждый этап обучения этим навыкам сложения и вычитания на раннем этапе и запланировали интерактивные упражнения, чтобы помочь вашим ученикам овладеть ими. Независимо от того, используете ли вы физические блоки, моделируете наши упражнения на доске или заставляете учащихся входить в свою учетную запись для работы в Интернете, эти стратегии обеспечат успех в вашем классе.

Проверьте эти и другие упражнения в своем аккаунте Happy Numbers.

Впервые в Happy Numbers? Узнать больше!

Бонус: использование числовых строк

Как видите, блоки с основанием 10 — отличное представление чисел для юных учеников. Они особенно полезны при обучении складывать и вычитать до 10.Однако, как только ваши ученики достигнут этого уровня, блоки base-10 имеют определенные ограничения. Например, большее количество означает большее количество материалов. Представление уравнений в виде блоков — медленный процесс. Вы не можете представить десятичные дроби или отрицательные числа с помощью блоков.

Вот почему важно сбалансировать эту модель с другими опциями. Например, числовая линия — еще одна полезная модель. В Happy Numbers мы чередуем упражнения, использующие блоки с основанием 10, с упражнениями с использованием числовой прямой.Вы можете прочитать больше здесь, а пока вот несколько идей о том, как использовать числовую строку для поддержки обучения сложению до 10.

Сначала мы моделируем уравнение с числовой линией, обозначенной всеми числами 0-20:

Затем мы увеличиваем сложность, отмечая только 0 и 20. По мере того, как учащиеся работают над уравнением, появляются другие метки:

Та же стратегия применяется для вычитания:

—
С уважением,
Команда Happy Numbers

Отбросьте базу 10 блоков

Просто выброси их уже в мусорное ведро.

{Этот пост содержит партнерские ссылки.}

Ok. Позвольте мне вернуться … #longpostalert

Более 20 лет назад — ДВАДЦАТЬ ЛЕТ — Я сидел в классе 5-го класса, когда кто-то принес * огромную * коробку оранжевых деревянных блоков из 10 блоков. Мой учитель 5-го класса выиграл грант, и мы получили бесплатные инструменты по математике! Так весело и так захватывающе!

Но это было 20 лет назад. Когда манипуляторы только изучались как способ помочь детям понять математику.

2 года назад я слушал Линду Джаслоу, моего инструктора по математике на уроке лидерства по математике, в котором я участвую процитировать Линду Гриффит (известный исследователь компьютерной графики),

«Никакой математический инструмент не должен думать за детей.«

И это изменило мое отношение к математическим манипуляторам. В частности, базовые 10 блоков.

Видите ли, проблема была в том, что мои первоклассники использовали базовые 10 блоков для чего угодно, НО математики. Во время наших математических загадок мои дети были супер-накачаны, чтобы схватить эти блестящие синие блоки с основанием 10, а затем использовали десять стержней, чтобы представить друга, о котором была их математическая загадка, или, что еще хуже … использовали стержень с десятью, чтобы представить один из что-то, счетная метка, номер один …

И да, я потратил добрых 5-10 минут каждый день работая над разбиением чисел на десятки и единицы с интерактивными базовыми 10 блоками во время Математической стены.И они полностью узнали, сколько стержней и кубиков можно использовать для построения двухзначных чисел — даже трехзначных чисел.

Но действительно ли они понимали нашу систему base 10?

Не думаю. Даже не близко. Потому что они не могли использовать базовые 10 блоков, чтобы помочь им решать математические задачи самостоятельно … ну, кроме, может быть, 2 детей из 25.

Мы потратили большую часть прошлогоднего урока лидерства по математике, рассказывая о нашей базе 10 и насколько важно для детей понимать основание 10, чтобы иметь возможность успешно складывать, вычитать, умножать и делить с пониманием .

Итак, в чем дело? Почему не работают блоки base 10?
Потому что ими нельзя манипулировать и изменять. Дети не могут построить свою собственную группу из десяти человек, им просто нужно знать, что захват 1 удочки десять — это то же самое, что захват 10. И это действительно, действительно , трудно освоить. Как учитель, я не могу просто сказать им, что 1 штанга десять — это то же самое, что взять 10 и ожидать, что они поймут. Чтобы понять это, нужно много экспериментировать с подсчетом и группировкой объектов.А если им нужно разделить десять, чтобы вычесть? Забудь об этом. Вы можете в значительной степени рассчитывать на своего обычного первоклассника, который заберет все десять удочек вместо того, чтобы пытаться обменять их на одни и забрать только часть.

Если вы хотите быть учителем, который просто учит детей шагам и позволяет им копировать вас, тогда хорошо. Это может сработать. Но если вы хотите, чтобы ваши первоклассники понимали и могли складывать и вычитать 2- и 3-значные числа самостоятельно без вашей помощи в запоминании нескольких шагов ?? Да, с базовыми 10 блоками этого не случится…. по крайней мере, пока они не поймут систему счисления 10.

Хорошо, хорошо. Я разнесу базовые 10 блоков. Что теперь? В прошлом году я воспользовался предложением Math TOSA в нашем районе и превратил свои поп-кубы в группируемые «базовые 10 блоков». Взяв базовые 10 блоков {и, ммм, фактически не выбрасывая их в мусорное ведро … почти уверен, что я их не покупал, и это было бы большим «нет-нет». Я просто спрятал их в хранилище!}, Я раздал каждой группе наши бадьи с поп-кубиками (мои любимые поп-кубики можно найти здесь!).На самом деле они уже были на полке для детей, чтобы использовать их во время математических загадок, но, честно говоря … они все равно не использовали их в качестве инструментов. Поп-кубы хороши для одного и только для 6-летних детей: для строительства башен. И пистолеты. Ладно, может быть, это две вещи …

Снова на ходу … после раздачи кубиков со вкусом я попросил детей построить число 48 наиболее эффективным способом. Так что всякий раз, когда я считаю их кубики, мне было легко и быстро считать. Я выбрал 48, потому что это число, которое большинство моих детей может построить в начале года, когда мы это сделаем, и потому, что оно достаточно высокое, что просто построить башню из 48 становится проблемой, и несколько детей попытаются разбить башню на группы. .Дав им несколько минут на создание числа, мы рассказали, как построили 48. Многие из моих первокурсников построили большую длинную башню. {{РЕДАКТИРОВАТЬ 9/2015: Это фотографии из той же задачи в следующем году, так как у меня не было фотографий во время этой исходной публикации.}}

Некоторые сделали «твари …»

И некоторые БУКВАЛЬНО сделали число 48 …
Но некоторые начали ломать башню.

Когда мы сделали это в начале сентября, у меня было двое детей, которые составляли группы по 5 человек, и ни один ребенок не составлял группы по 10 человек.{Картинка выше — это редактирование следующего года, когда у меня была какая-то группа по 10 человек}

Я надеялся, что кто-то сделает группы по 10 человек, но, эй, иногда тебе просто нужно использовать то, что у тебя есть! И все это было предсказуемо и приемлемо для моих целей урока: найти несколько способов получить одно и то же число и найти наиболее удобный способ построить число.

Во-первых, мы разделили 48 причудливой формы одного ребенка.

Я указал, что у него 4 здесь, 12 здесь и т.д … и затем спросил, была ли форма сделана удобным способом для подсчета? {НЕТ….} Я спросил: «Как мы можем расположить 48 кубиков так, чтобы они были полезны для подсчета?» Некоторые из моих первоклассных ответов: «Я все время теряю из виду, где мы находимся!» «Я не вижу этого куба!» Помните, что этот урок проходит в сентябре, поэтому уровень понимания не такой высокий, как если бы я сделал этот же урок сейчас! 🙂

Затем я поделился башней другого ребенка, и мы поговорили о том, сколько времени потребуется, чтобы сосчитать до 48, если все пересчитать ВСЕ 48 кубиков по одному. Я спросил: «Полезно ли считать все 48 кубиков по одному? Как мы можем расположить кубики так, чтобы они были полезны для счета?» Некоторые первые ответы: «Мы могли считать по 2! Или 5! Или 10!»

Я поделился девушкой, которая разбила свою на группы по 5 человек.Мы посчитали ее по 5, а затем по единице. Мы все согласились, что это быстрее и полезнее. Затем я спросил: «Есть ли другой способ, который был бы еще быстрее?» Мой высший математический мыслитель спас положение и сказал: «ДЕСЯТКИ !!!!» Слава богу, этим старшим детям. Они помогают вести наш разговор, когда мы собираемся сделать несколько революционных математических открытий, и помогают облегчить понимание других.

#thestruggleisreal

Я уже планировал, что никто не придет в голову считать по 10…. вот план на случай, если это случится с вами: «Вы сказали, что мы можем считать по 5/2. Что еще мы умеем считать по? (10) Можем ли мы составить группы по 10 кубиков, чтобы мы могли считать по 10? »

Когда дети обнаружили, что счет по 10 будет быстрее, я попросил каждого ученика построить свои 48 кубиков, разбивая группы по 10. Мы сделали это вместе и тщательно обсудили оставшиеся 8 наших и то, как они не составляют полную группу из 10 человек. К этому моменту все мои первоклассные были на подножке 10! Итак, я попросил каждую группу разделить все кубики поп-куба из ванны своей группы на группы по 10 штук, а оставшиеся кубики оставили как единицы.Затем я сказал им, что мы будем держать наши кубики таким образом сгруппированными в течение всего года. Когда они убирают после задач по математике, они должны убедиться, что кубики находятся в их группах по 10 штук. Мы только вкратце говорили о том, насколько более полезным будет этот инструмент при построении большого числа («Вы можете построить его быстрее», «Теперь я могу просто считать по десяткам!» …)

. следующий. день. во время задач по математике у большинства моих детей были эти кубики, чтобы сложить наши двухзначные числа из нашей математической задачи!

Что ж, это здорово. Но чем это отличается от моих симпатичных блоков Base 10? Основная причина, по которой поп-кубики лучше, заключается в том, что дети могут сами строить и ломать десятки. И поскольку я начинаю год с того, что их разбивают на группы по 10 человек, они лучше понимают, что их жезл поп-кубиков — не один. Это 10. Гибкость, позволяющая взломать и построить 10, ТАК полезна. Я наблюдал, как школьники (не только мои старшие дети) должны были добавить еще 9, взять 10 и просто убрать один кубик вместо того, чтобы отсчитывать 9.Это ДЕЙСТВИТЕЛЬНО важная идея для детей — иметь возможность разложить 10. И это то, чего вы не получите с помощью обычных блоков ole base 10.

Так вы, серьезно, больше никогда не используете красивые блоки Base 10? Нет, правда нет. Ну вроде как. Я до сих пор делаю математическую стену, по которой скользят интерактивные блоки с базовыми 10 блоками примерно раз в неделю, но мы редко проходим слайды с базовыми 10 блоками. И когда мы это делаем, мы просто используем это для гибкости — сколько способов мы можем построить число 76 с десятками и единицами.Они также практикуют слайд по базе 10 во время своего занятия на стене по математике во время наших станций и группового чтения с гидом. Но мы не тратим много времени на математические инструкции по базовым 10 блокам. Фактически, я осмелюсь сказать, что в этом году мое прямое обучение по блокам с базой 10 наверняка было меньше часа … возможно, даже меньше 30 минут.

Почему я не часто использую математические настенные слайды из 10 блоков? Потому что моим детям это не нужно. Потому что использование поп-кубов в качестве группируемого манипулятора с основанием 10 помогло укрепить их понимание десятков и единиц, и большей части моего класса просто больше не нужна практика с этим.В прошлый День святого Валентина я скопировал загруженную рабочую страницу, которую нашел где-то на Pinterest (не могу найти исходный источник), для вечеринки. Дети должны были сосчитать картинки из 10 кубиков и раскрасить число на диаграмме сотен, чтобы раскрыть секретную картинку — сердце. Ни один — ни ОДИН — ребенок в моем классе не боролся с этим. Нет. Один. Даже самые младшие дети могли сосчитать базовые 10 блоков и записать число в поле. Может быть, я должен был быть шокирован этим, учитывая нехватку учебного времени, потраченного на блоки базовой 10 и несуществующие блоки базовой 10 в нашем классе…. но я совсем не был шокирован. Потому что, когда вы преподаете для понимания основы 10 вместо обучения инструментам основы 10, вы получаете больше отдачи от вложенных средств. И ваши дети могут овладеть всеми теми низкоуровневыми навыками, над которыми многие учителя тратят весь год, работая со своими детьми. Нет проблем для ребенка, у которого есть сильное понимание по основанию 10!

Хорошо, я понял. Итак, что еще, кроме поп-кубиков, вы используете, чтобы научить «размещать ценность»? Я провожу много учебного времени, помогая своим детям развить понимание основы 10.Помимо выбора наборов чисел, которые помогают с основанием 10 во время математических загадок и кубиков, есть еще несколько других регулярных действий, которые действительно помогают с основанием 10.

1. Подсчет коллекций:

Вы можете прочитать мой подробный блог о процедурах и процедурах подсчета сборов ЗДЕСЬ. Когда детям приходится считать большие числа каждую неделю, они начинают группировать свои коллекции в группы по 5, 10 или даже 20, чтобы более эффективно считать. Создание групп по 10 человек снова и снова помогает укрепить понимание того, что 10 человек — это то же самое, что и 1 группа из 10 человек.Он также отлично подходит для того, чтобы дать детям множество различных визуальных эффектов (помимо 10-го стержня) для группы из 10 … десять зубочисток, десять пенни, десять по прямой, десять в круговой группе, десять в стопке пуговиц …

2. Math Talks:

В книге Number Talks и в моем соответствующем пакете есть целый раздел, в котором рассказывается о числах для создания десятков. Каждый мини-урок создан для того, чтобы дети наглядно увидели, как сделать так, чтобы группа из десяти человек считала более эффективно. В каждом разделе также есть десять разговоров с номерами кадров, которые мне также нравятся за визуальное представление группы из десяти человек.Из всех разговоров о числах именно эти я использую чаще, чем любые другие.

3. Математические игры:

Эти наборы игр специально разработаны с учетом понимания основы 10. Конечно, многие из них существуют в течение многих лет и не являются моей первоначальной идеей, но я обнаружил, что использование раздаточных материалов, которые я включил для записи, действительно помогает с пониманием основы 10, а также просто старой подотчетностью! * wink *

Итак, сделайте глубокий вдох, найдите все эти кадки из блоков base 10 и пожертвуйте их другому учителю, у которого не хватит смелости выбросить их.Или положите их во внутренние ниши. Или положите их в шкаф для хранения математики в школе. Или, или, или ….

Только не используйте их больше! Ты можешь это сделать! Вы станете лучшим учителем для этого, и ваши дети тоже станут лучшими наркоманами по математике!

Руководство по оценке

| Мартинсвилл Бетон

Рисунки, показанные ниже, предназначены только для практического использования.
Кол-во единиц

• 2 1/2 High Block (2 ^1/4 x8x16) –3.10 блоков на площадь стены
• Half High Block (4x8x16) –2,25 блока на площадь стены
• Стандартный блок (4 дюйма, 8 дюймов, 10 дюймов, 12 дюймов) — 1,125 блока на площадь стены
• Кирпич лицевой модульный — 7,0 кирпича на площадь стены
• Кирпич негабаритный — 6,0 кирпича на площадь стены
• Кирпич кладочный — 3,0 кирпича на площадь стены

Количество минометов

• Блок — 3 мешка на 100 блока
• Кирпич лицевой модульный — 7 пакетов на 1000 кирпичей
  Кирпич негабаритный — 8 пакетов на 1000 кирпичей
• Кирпич хозяйственный — 10 мешков на 1000 кирпича

Количество песка

• Песок – 1 тир. Год на 7 мешков раствора

Количество арматуры горизонтальной стены

• Горизонтальная арматура стен – SF / 1.33

Количество изоляционного материала для заполнения полости

• Изоляция заполнения полости — 4 CF на мешок

Приблизительный объем, необходимый для заполнения пустот керна в блоке

• 6x8x16 2 ядра 0,17 CF / блок
• 8x8x16 2 ядра 0,25 CF / блок
• 10x8x16 2 ядра 0,33 CF / блок
• 12x8x16 2 ядра 0,39 CF / блок

Приблизительное количество бетона, необходимое для заполнения связывающих балок

• 6x8x16 BBL 0.Бетон 173 CF согласно LF
• 8x8x16 Бетон BBL 0,22 CF согласно LF
• 8x8x16 DEEP BBL 0,46 CF бетон согласно LF
• 12x8x16 Бетон BBL 0.37 CF согласно LF
• 12x8x16 DEEP BBL 0,74 CF бетон согласно LF

Количество блоков на куб
Размер	Арка PSF Нет на куб	Арка PSMF No Per Cube	Arch GF Нет на куб	Redline TM UL LT Вес Нет на куб Нет на куб
2 1/4 x4x16	270	–	–	–
4x4x16	240	240	288	300
4x8x16	120	120	144	150
6x4x16	100	100	120	120
8x8x16	75	75	90	90
12x8x16	50	50	60	60

Типичные размеры бетонной кладки
Номинал		Фактический размер блока		Лицевая оболочка Толщина (a)		Паутина Толщина (а)
дюймов — фунтов	Метрическая система	дюймов — фунтов	Метрическая система	дюймов — фунтов	Метрическая система	дюймов — фунтов	Метрическая система
(дюйм. )	(мм)	(дюймы)	(мм)	(дюймы)	(мм)	(дюймы)	(мм)
4x8x16	102x203x406	3 5/8 x7 5/8 x15 5/8	92x194x397	3/4	19	3/4	19
6x8x16	152x203x406	5 5/8 x7 5/8 x15 5/8	143x194x397	1	25	1	25
8x8x16	203x203x406	7 5/8 x7 5/8 x15 5/8	194x194x397	1 1/4	32	1	25
10x8x16	254x203x406	9 5/8 x7 5/8 x15 5/8	244x194x397	1 3/8	35	1 1/8	29
12x8x16	305x203x406	11 5/8 x7 5/8 x15 5/8	295x194x397	1 1/2	38	1 1/8	29
(a) Размеры соответствуют минимальным требованиям ASTM C 90 (a) (ссылка, 3).

Проектирование стен во избежание резания агрегатов на рабочих местах

Правило 1. Размер в четном количестве футов (2 фута, 4 фута, 6 футов и т. Д.) Всегда будет работать в полном или полублочном блоке.
Правило 2. Размер в четном количестве футов плюс 8 дюймов (2 фута 8 дюймов, 4 фута 8 дюймов, 6 футов 8 дюймов и т. Д.) Всегда будет работать полностью. и полублок.

Правило 3. Размер в нечетном количестве футов (1 фут., 3 фута, 5 футов и т. Д.). не закончится полным-полублоком. Но нечетное количество футов плюс 4 дюйма (1 фут 4 дюйма, 3 фута 4 дюйма, 5 футов 4 дюйма и т. Д.) Всегда будет работать в полном и половинном блоке.

Примеры неправильной и правильной планировки проемов в бетонных стенах

Иллюстративная математика

IM Комментарий

Эта задача представляет собой пример квадратичной функции. Другие задачи в этом наборе иллюстрируют Ф.BF.1a в контексте линейных (Кими и Джордан), экспоненциальных (слухи) и рациональных (Summer Intern) функций.

Это основано на задаче, разработанной командой MARS / Shell Center. Служба ресурсов по оценке математики (адаптирована с разрешения для распространения с лицензией Creative Commons в этой форме).

Решения

Решение: Арифметическая последовательность, вариант 1

В этом решении мы считаем кубики рядами (или слоями):

1. Верхний слой состоит из одного куба.Слой ниже имеет один кубик ниже верхний куб плюс 4 доллара за новые, что в сумме составляет 5 долларов. Третий слой ниже содержит кубики ниже этих 5 долларов плюс новые 4 доллара, чтобы получить 9 долларов. Продолжая добавлять по четыре каждый раз, мы получаем в сумме $$ 1 + 5 + 9 + 13 + 17 + 21 = 66 $$ кубы в скелетной башне с шестью слоями.
2. Основываясь на рассуждениях, установленных в а), количество кубиков внизу (12 $ т.) слой будет $ 1 + 4 \ times 11 $, так как он находится на $ 11 $ слоев ниже верхнего. Итак, для этого нам нужно Добавить $$ 1 + 5 + 9+ \ ldots + 45.$$ Один из способов сделать это — просто сложить числа. Более быстрый метод, который для любого количества слоев будет работать так называемый метод Гаусса (который математик, как сообщается, суммировал большой список целых чисел, когда он был очень молодой). Идея состоит в том, чтобы переписать сумму в обратном порядке как $$ 45 + 41 + 37 + \ ldots + 1. $$ Теперь, если этот список поместить под предыдущим списком, мы увидим, что сумма каждого столбца равна 46 $. Столбцов $ 12 $, поэтому ответ на эту проблему составляет половину от $ 12 \ times 46 = 552 $ или 276 $.{\ rm th} $ слой отсчитывает сверху вниз. потом $ f (1) = 1 $ — количество кубиков в верхнем слое, $ f (2) = 5 $ — количество кубиков во втором слое сверху и так далее. В этом случае значения функции $ f (1), f (2), f (3), \ ldots $ образуют арифметическая последовательность, где каждый член получается из предыдущего добавлением 4 $. В общем, имеем $ f (n) = 4 (n-1) + 1 $. Метод, использованный для решения задачи b), обеспечивает метод как решения проблемы каркасной башни, так и добавления общей арифметической последовательности.Для задачи скелетной башни с $ n $ слоями в башне сумма, дающая общее количество кубов, будет $$ 1 + 5 + 9 + \ cdots + f (n) = 1 + 5 + 9 + \ cdots + (4 (n-1) +1). $$ Если мы воспользуемся здесь методом задачи б), удвоенная сумма будет равна $ n (4 (n-1) +2) $ и, следовательно, общее решение для количества кубиков в скелете башня с $ n $ слоями $$ \ frac {n (4 (n-1) +2)} {2} = n (2n-1). $

Решение: Арифметическая последовательность, вариант 2

В этом решении мы считаем кубики столбцами.

1. Верхний слой состоит из одного куба, а под ним находятся пять слоев кубиков. один из кубиков на общую сумму 6 долларов в столбце с верхним. Следующий уровень представляет 4 доллара. новых кубов и четыре слоя ниже, так что это дает в общей сложности 20 $ кубов в этих Столбцы $ 4 $. Точно так же каждый последующий слой вводит 4 новых столбца, поэтому мы вычисляем общую сумму, которая будет $$ 6 + 4 \ раз 5 + 4 \ раз 4 + 4 \ раз 3 + 4 \ раз 2 + 4 \ раз 1 = 66. $$
2. Имитируя метод, использованный в первой задаче, мы обнаруживаем, что столбец под кубик сверху состоит из 12 кубиков.Затем идут четыре столбца по 11 кубиков. высокий, четыре столбца по 10 кубов и так далее до четырех столбцов которые имеют высоту в один куб. Добавление всего этого дает $$ 12 + 44 + 40 + \ ldots + 4. $$ Мы можем упростить это до $$ 12 + 4 (11 + 10 + \ ldots + 1).