Схемы замещения трансформаторов: 1.7. Схема замещения трансформатора

Содержание

1.7. Схема замещения трансформатора

Составление схемы замещения. Систему уравнений (1.20) – (1.22), описывающую электромагнитные процессы в трансформаторе, можно свести к одному уравнению, если учесть, что , и положить

(1.26)

При этом параметры R₀ и X₀ следует выбирать так, чтобы в режиме холостого хода, когда ЭДС E₁ практически равна номинальному напряжению U₁, ток

(1.27)

по модулю равнялся бы действующему значению тока холостого хода, а мощность – мощности, забираемой трансформатором из сети при холостом ходе.

Решим систему уравнений (1.20) – (1.22) относительно первичного тока

(1.28)

В соответствии с уравнением (1.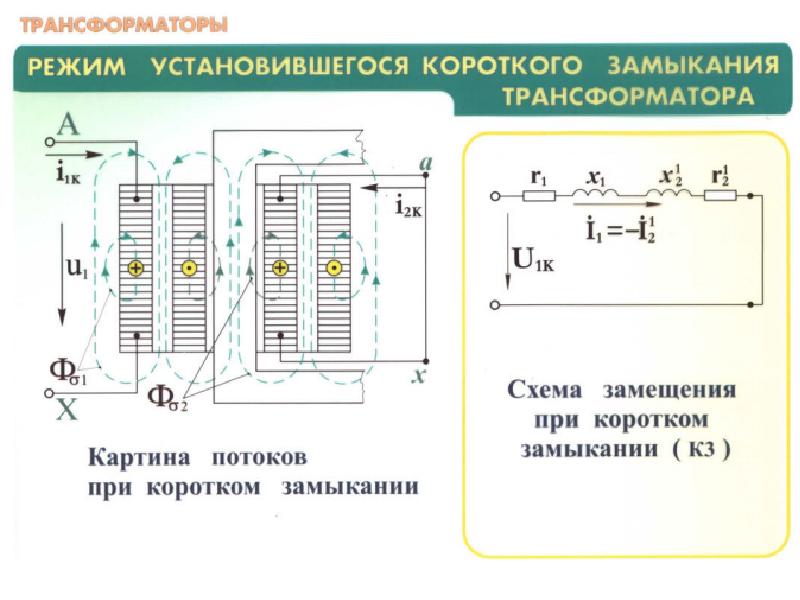

28) трансформатор можно заменить электрической схемой, по которой можно определить токи Í₁ и Í₂, мощность P₁, забираемую из сети, мощность ΔP потерь и т.д. Такую электрическую схему называют схемой замещения трансформатора (рис.1.9).

Рис. 1.9

Эквивалентное сопротивление этой схемы

(1.29)

где: ; ; ; .

Схема замещения трансформатора представляет собой сочетание двух схем замещения — первичной и вторичной обмоток, которые соединены между собой в точках а и б. В цепи первичной обмотки включены сопротивления R₁ и X₁, а в цепи вторичной обмотки – сопротивления R′₂ и X′₂. Участок схемы замещения между точками а и б, по которому проходит ток I₁₀, называют намагничивающим контуром. На вход схемы замещения подают напряжение Ú

1, к выходу ее подключают переменное сопротивление нагрузки , к которому приложено напряжение –Ú′₂.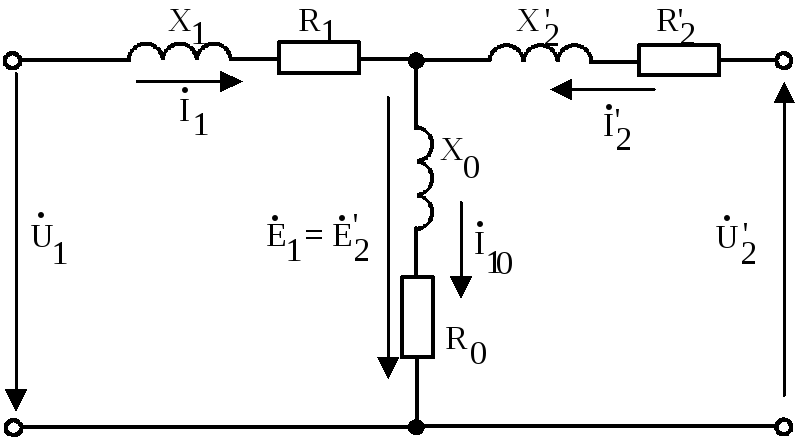

Сопротивления (и его составляющие R′₂ = R₂ n² и X′₂ = X₂n² ), а также называют соответственно сопротивлениями вторичной обмотки и нагрузки, приведенными к первичной обмотке. Аналогично приведенными называют значения ЭДС и тока : E′₂ = nE₂ ; .

Полная мощность приведенного контура вторичной обмотки в схеме замещения равна мощности вторичной обмотки реального трансформатора: I′₂ E′₂= (I₂/n )E₂n = E₂ I₂, а мощность электрических потерь в приведенном вторичном контуре этой схемы равна мощности потерь во вторичной обмотке реального трансформатора:

Относительные падения напряжений в активном и индуктивном сопротивлениях приведенного вторичного контура также остаются неизменными, как и в реальном трансформаторе:

; .

1.8. Определение параметров схемы замещения

Параметры схемы замещения для любого трансформатора можно определить по данным опытов холостого хода (рис. 1.10) и короткого замыкания (рис. 1.12).

Опыт холостого хода

В опыте холостого хода (рис. 1.10) вторичная обмотка трансформатора разомкнута, а к первичной подводится номинальное напряжение U_1н= U₁₀.

Рис. 1.10

Схема замещения трансформатора (рис. 1.9) для режима холостого хода (I₂=0) примет вид (рис. 1.11).

Рис. 1.11

Измерив ток холостого хода I₁₀ и мощность P₁₀, потребляемую трансформатором, согласно схеме замещения (рис. 1.11,а) находим

(1.30)

где: Z_вх
х – входное сопротивление трансформатора при опыте холостого хода.

Так как ток холостого хода мал по сравнению с номинальным током трансформатора, электрическими потерями ΔP_эл1 = I²₁₀R₁ пренебрегают и считают, что вся мощность, потребляемая трансформатором, расходуется на компенсацию магнитных потерь в стали магнитопровода. При этом

(1.31)

откуда R₀ = P₁₀/ I²₁₀.

Аналогично считают, что X₁ + X₀ ≈ X₀, так как сопротивление X₀

определяется основным потоком трансформатора Ф (потоком взаимоиндукции), а X₁ – потоком рассеяния Ф_Δ1, который во много раз меньше Ф. Поэтому с большой степенью точности полагают, что

(1.32)

Z₀ = U₁₀ / I₁₀; .

Измерив напряжения U₁₀ и U₂₀ первичной и вторичной обмоток, определяют коэффициент трансформации

(1.33)

n = U₁₀ / U₂₀.

Векторная диаграмма трансформатора в режиме холостого хода, построенная исходя из указанных выше допущений, изображена на рис. 1.11, б. В действительности ток Í₁₀ создает в первичной обмотке падения напряжения Í₁₀ R₁ и j Í₁₀ X₁, поэтому .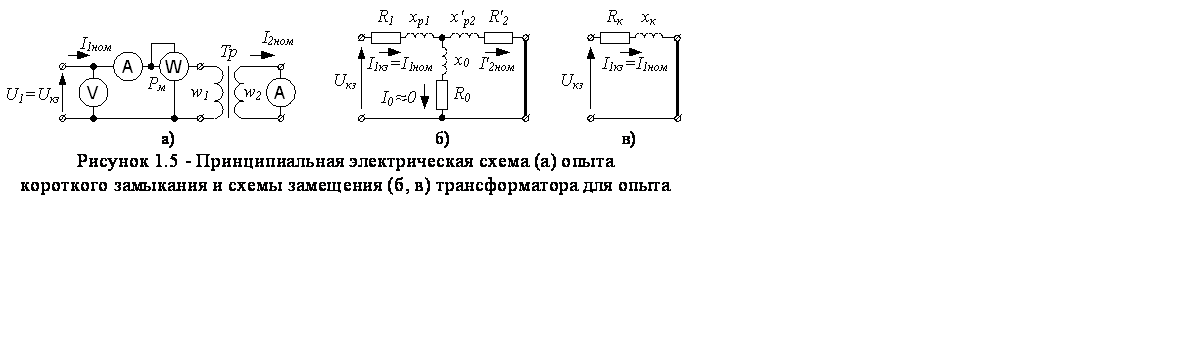 Соответствующая векторная диаграмма показана на рис. 1.11, в.

Опыт короткого замыкания

Вторичную обмотку замыкают накоротко сопротивление Z_н = 0), а к первичной подводят пониженное напряжение (см. рис.1.12) такого значения, при котором по обмоткам проходит номинальный ток I_ном. В мощных силовых трансформаторах напряжение U_к при коротком замыкании обычно составляет 5-15% от номинального. В трансформаторах малой мощности напряжение U_к может достигать 25-50% от U_ном.

Рис. 1.12

Так как поток, замыкающийся по стальному магнитопроводу, зависит от напряжения приложенного к первичной обмотке трансформатора, а магнитные потери в стали пропорциональны квадрату индукции, т.е. квадрату магнитного потока, то ввиду малости U_к пренебрегают магнитными потерями в стали и током холостого хода. При этом из общей схемы замещения трансформатора исключают сопротивления R₀ и X₀ и преобразуют ее в схему, показанную на (рис 1.

13, а). Параметры этой схемы определяют из следующих соотношений:

(1.34)

Схема замещения трансформатора | Электротехника

Введение. В электрических цепях обмотки трансформаторов связаны между собой магнитным полем. Это усложняет расчет цепи и анализ ее работы.

Поэтому целесообразно заменить трансформатор его моделью, которая называется схемой замещения. Построение схемы замещения должно удовлетворять требованиям, предъявляемым к моделям, т. е. математическое описание режима схемы замещения должно совпадать с математическим описанием электрического состояния трансформатора.

Схема замещения для приведенного трансформатора. Приведенный трансформатор математически описывается уравнениями электрического состояния (2.8), (2.10) и уравнением токов (2.6б). В соответствии с этими уравнениями построена схема замещения трансформатора (рис. 2.9).

На схеме и соответственно — активное сопротивление и сопротивление рассеяния первичной обмотки; и — приведенные активное сопротивление и сопротивление рассеяния вторичной обмотки; и — активное и реактивное сопротивление ветви холостого хода.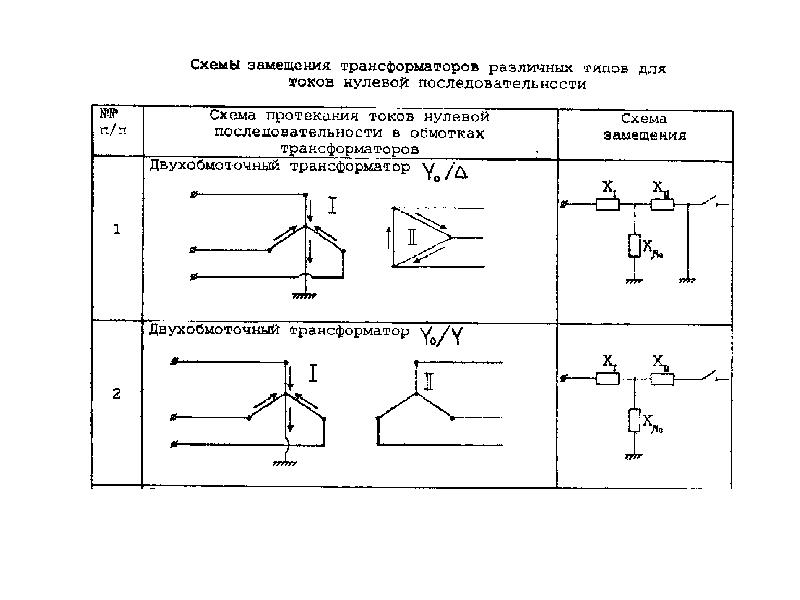 Мощность потерь в сопротивлении при токе эквивалентна потерям в магнитопроводе, т.е. – эквивалентное реактивное сопротивление. Падение напряжения на ветви холостого хода с комплексным сопротивлением при токе равно ЭДС и трансформатора.

Упрощенная схема замещения.

Параметры схемы замещения трансформатора экспериментально найти трудно. Если пренебречь током холостого хода из-за его малости, то получим так называемую упрощенную схему замещения (рис. 2.10), где

и называются сопротивлениями короткого замыкания

и (2.11)

Схема замещения трансформатора

Подробности: Категория: Теория

Уравнениям (8) и (9) соответствует электромагнитная схема замещения (рис. 6).
Для выполнения аналитических расчетов трансформатора магнитную связь между обмотками удобно заменить электрической. С этой целью вторичную обмотку трансформатора необходимо привести к первичной по числу витков. Формально приведение осуществляется путем умножения второго уравнения системы (8) на коэффициент трансформации :

, (10)

где — приведенное значение напряжения вторичной обмотки.
Из условия равенства мощностей приведенной и неприведенной обмоток

получаем выражение для приведенного тока:
.                  (11)
С учетом этого выражения уравнение (10) приобретает вид
,                                     (12)
где ;                       .
Реактивная составляющая намагничивающего тока приведенного трансформатора определяется суммой токов,
.
Если теперь уравнения приведенного трансформатора записать в виде

(13)
и учесть, что , то электромагнитную связь в схеме (рис.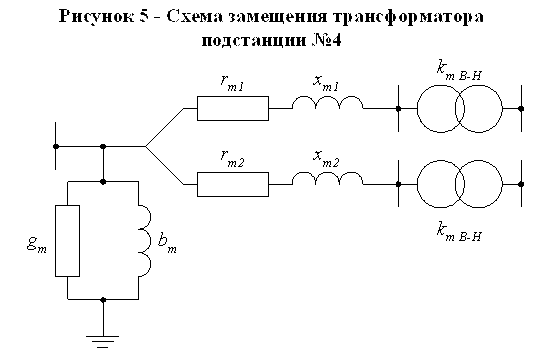 6) можно заменить электрической (рис. 7).

Схема замещения трансформатора (рис. 7) является его расчетной схемой при анализе как установившихся, так и переходных процессов.
При синусоидальных напряжениях и токах для описания установившихся режимов вместо дифференциальных уравнений удобнее пользоваться комплексными уравнениями для действующих значений токов и напряжений. Чтобы получить комплексные уравнения трансформатора, нужно заменить на :

                                            (14)
Введем обозначения:
        — индуктивное сопротивление взаимной индукции;
     — индуктивное сопротивление рассеяния первичной обмотки;
    — индуктивное сопротивление рассеяния вторичной обмотки;
— комплексное сопротивление первичной обмотки;
— комплексное сопротивление вторичной обмотки.
Уравнения в новых обозначениях имеют вид
                                                    (15)
При выводе уравнений трансформатора предполагалось, что процесс намагничивания сердечника не связан с потерями энергии на гистерезис и вихревые токи. Их можно учесть приближенно, приняв допущение, что потери в стали пропорциональны следующим величинам:
,
отсюда ясно, что потери в стали можно учесть, если параллельно сопротивлению включить активное сопротивление (рис. 8, а). При расчетах удобно параллельные ветви свернуть в одну ветвь (рис. 8, б) с активным сопротивлением:

и индуктивным сопротивлением
.
Тогда уравнения трансформатора с учетом потерь в стали примут вид

, (16)

где .
Уравнениям (16) соответствует Т-образная схема замещения приведенного трансформатора, представленная на рис. 9.
Численные расчеты по уравнениям (16) и соответствующей им схеме замещения (рис. 9) обычно выполняют в относительных единицах. В качестве базисных принимаются
— действующее значение номинального фазного напряжения первичной обмотки;
— действующее значение номинального фазного тока первичной обмотки;
— фазное сопротивление номинальной нагрузки.
Переход к относительным единицам осуществляется путем деления величин в именованных единицах на соответствующие базисные значения.
Сопротивления трансформатора в относительных единицах имеют следующий порядок:
; ;
;
Необходимо отметить, что сопротивления и не являются постоянными. Они зависят от насыщения магнитопровода. Остальные сопротивления можно считать практически постоянными для всех режимов работы трансформатора.

Схема замещения трансформатора — презентация онлайн

Параметры первичной обмотки трансформатора
отличаются от параметров вторичной обмотки, что
при больших коэффициентах трансформации
затрудняет расчеты и построение векторных
диаграмм. Указанные затруднения устраняются
приведением всех параметров трансформатора к
одинаковому числу витков, обычно к числу витков
первичной обмотки w1. Для этого величины,
характеризующие вторичную цепь трансформатора,
пересчитывают на число витков w1 первичной
обмотки.

Вместо реального трансформатора с коэффициентом
трансформации k = w1/w2 получают эквивалентный
трансформатор с k=w1/w’2=1, где w’2=w1. Такой
трансформатор называют приведенным.
Приведение вторичных параметров трансформатора
не должно отразиться на его энергетических
показателях: все мощности и фазовые сдвиги во
вторичной обмотке приведенного трансформатора
должны остаться такими, как и в реальном
трансформаторе.
Электромагнитная мощность вторичной обмотки
реального трансформатора Е2I2 должна быть равна
электромагнитной мощности вторичной обмотки
приведенного трансформатора:
E2 I 2 E2 I 2 .
Соответственно для остальных электрических
величин:
E2
I2
I 2 w1
w1
E2
E2 E2
.
I 2
I 2 w2
w2
U 2 U 2 (w1 / w2 ).
Из условия равенства потерь в активном и реактивном сопротивлении вторичной обмотки имеем
I 22 r2 I ‘ 22 r ‘ 2
r2 r2 ( I 2 / I 2 ) 2 r2 (w1 / w2 ) 2 .

x2 x2 ( w1 / w2 ) 2 .
Приведенное полное сопротивление вторичной
обмотки трансформатора
Z 2 r2 jx2 (r2 jx2 )( w1 / w2 ) 2 Z 2 (w1 / w2 ) 2 .
Приведенное полное сопротивление нагрузки
Z н Z н ( w1 / w2 ) 2 .
Уравнения напряжений и токов для
приведенного трансформатора имеют вид
U 1 ( E 1 ) I 1Z1 ( E 1 ) jI 1 x1 I 1r1 ;
U 2 E 2 I 2 Z 2 E 2 jI 2 x2 I 2 r2 ;
I I ( I ).
1
0
2
Данные
уравнения
устанавливают
аналитическую
связь
между
параметрами
трансформатора во всем диапазоне нагрузок от
режима х.х. до номинальной.

5. Схема замещения трансформатора

Трансформатор можно представить электрической
схемой замещения. По этой схеме определяют токи
мощность P1, забираемую из сети, мощность потерь ΔР
и т. п.
Схема замещения трансформатора — сочетание
двух схем замещения — первичной и вторичной
обмоток, соединенных между собой. В цепи первичной
обмотки включены сопротивления R1 и X1, в цепи
вторичной R’2 и Х’2.

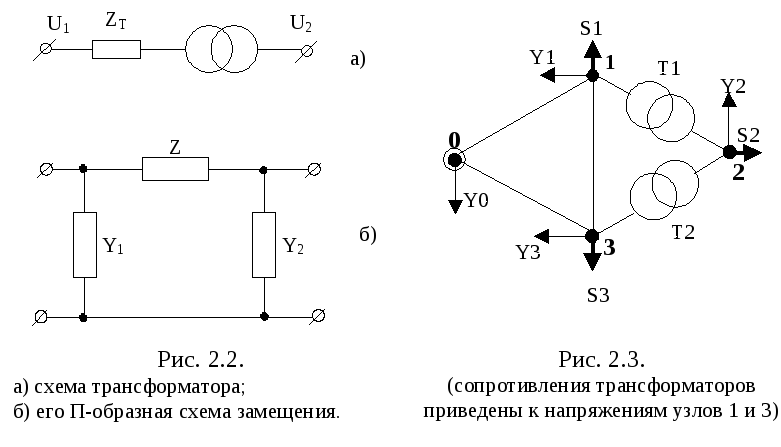Участок схемы замещения между
точками а и б, по которому проходит ток I0, называют
намагничивающим
контуром.
Схема
замещения
составляется по уравнениям представленным выше.
Все параметры схемы замещения, за исключением
Z’H,
являются
постоянными
для
данного
трансформатора и могут быть определены из опыта
х.х. и опыта к.з.

7. Определение параметров схемы замещения

Параметры схемы замещения для любого
трансформатора можно определить по данным
опытов холостого хода (рис. а) и короткого
замыкания (рис.б)

8. Опыт холостого хода и короткого замыкания

9. Опыт холостого хода

К зажимам одной из обмоток посредством
регулятора напряжения (РН) подводят номинальное
напряжение
обмотке подключают
U 0 ; кUдругой
1ном
вольтметр (ее можно считать разомкнутой). Измерив
ток холостого хода и мощность , потребляемую
I0
P0
трансформатором,
согласно схеме замещения
находят
2
( R1 Rm ) .

Z1 Z m U 0 I 0 ; R1 Rm P0 I 02 ;
X1 X m
Z1 Z m
2
Так как ток холостого хода мал по сравнению с
номинальным током трансформатора, электрическими потерями пренебрегают и считают, что вся
мощность,
потребляемая
трансформатором,
расходуется на компенсацию магнитных потерь в
стали магнитопровода. При этом
P0 I 02 R1 Rm I 02 Rm ,
Rm P0 I 02 .
Аналогично считают, что X1+Xm≈Xm , так как
сопротивление Хт определяется основным потоком
трансформатора Ф, a X1 — потоком рассеяния Фσ1,
который во много раз меньше Ф.
Следовательно
Z m U 0 I 0 ; X m Z m2 Rm2 .
Измерив напряжения U0 и U20 первичной и
вторичной обмоток, определяют коэффициент
трансформации
k U 0 U 20

12. Схема замещения и векторные диаграммы трансформатора в режиме хх

13. Характеристики холостого хода

• При
увеличении
первичного
напряжения
насыщение
магнитопровода
увеличивается,
вследствие чего ток ХХ I0 растет быстрее, чем U0.

Поэтому Z0 и X0 с ростом U0 уменьшаются. Так
как P0 ~E2 ~ U2, а I02 растет быстрее U02, то R0 с
ростом U0 также уменьшается.
При ОКЗ к первичной обмотке подводят
пониженное напряжение Uк, при котором по
обмоткам проходит номинальный ток Iном. В
мощных силовых трансформаторах Uк при
ОКЗ обычно составляет 5… 15% от
номинального. В трансформаторах малой
мощности напряжение Uк может достигать
25…50% от Uном.
Так как Ф, зависит от U1, а магнитные
потери в стали квадрату индукции, т. е.
квадрату магнитного потока, то ввиду малости
Uк пренебрегают магнитными потерями в
стали и током хх. Из схемы замещения
исключают сопротивления Rm и Хт
Z k Z1 Z 2 U k I íîì ;
2
Rk R1 R2 Pk I íîì ;
2
2
X k X1 X 2 Z k Rk .
Обычно
принимают
схему
замещения
симметричной, полагая Z1 = Z’2 = 0,5Zк/
Треугольник ABC, образуемый векторами
активного, реактивного и полного падений
напряжения, называют треугольником короткого
замыкания
или
характеристическим
треугольником

17.

Векторная диаграмма и схема замещения трансформатора для ОКЗ Треугольник ABC, образуемый векторами
активного, реактивного и полного падений
напряжения, называют треугольником короткого
замыкания
или
характеристическим
треугольником. Катеты ВС и АС называют
соответственно реактивной и активной составляющими напряжения короткого замыкания.
В паспортах трансформаторов указывают
относительное
напряжение
короткого
замыкания при номинальном токе в процентах
от номинального напряжения:
uk % I íîì Z k U íîì 100.
• Можно выразить относительные значения его
активной и реактивной составляющих
u к .в % I ном Rk U ном 100; u к . р % I ном X к U ном 100.
uê .â uk cos k ; uk . p uk sin k ;
uk uk2.a uk2. p .
• По известному значению ик% можно определить
установившийся ток кз при номинальном
напряжении:
I k U ном Z k U ном u k %U ном 100I ном 100I ном u k % .
• Обычно в силовых трансформаторах
большой и средней мощности значение ик%
составляет 5.

.. 15%. Ток кз в в 7…20 раз
превышает номинальный. Как правило, чем
больше мощность и напряжение силового
трансформатора, тем выше напряжение
короткого замыкания ик%.

СХЕМЫ ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРОВ

Двухобмоточный трансформатор (рис. 2.10,а) можно представить в виде Г-образной схемы замещения (рис. 2.10,б)

Рис. 2.10. Двухобмоточный трансформатор:

а – условное обозначение; б – Г-образная схема замещения;

в – упрощенная схема замещения.

Продольная часть схемы замещения содержит r_т и x_т – активные и реактивные сопротивления трансформатора. Эти сопротивления равны сумме соответственно активных и реактивных сопротивлений фаз первичной и приведенной к ней вторичной обмоток. Следует отметить, что в приведенной схеме замещения отсутствует трансформация, то есть отсутствует идеальный трансформатор, но сопротивление вторичной обмотки приводится к первичной. Из курса «Электрические машины» известно, что приведенное сопротивление получают умножением реального сопротивления на квадрат коэффициента трансформации. В дальнейшем, если сети, связанные трансформатором, рассматриваются совместно, а параметры сетей не приводятся к одному базисному напряжению, то в схеме замещения трансформатора учитывается идеальный трансформатор.

Поперечная ветвь схемы определяется расходом мощности на намагничивание трансформатора.

Ветвь намагничивания состоит из активной и реактивной проводимостей g_т и b_т. Активная проводимость g_т соответствует потерям активной мощности в сердечнике трансформатора от тока намагничивания I_m (рис. 2.10,б). Реактивная проводимость b_т определяется магнитным потоком взаимоиндукции в обмотках трансформатора.

В расчетах электрических сетей двухобмоточные трансформаторы при U_В,ном £ 220 кВ представляют упрощенной схемой замещения (рис. 2.10,в). При этом вместо ветви намагничивания учитывается мощность, потребляемая на намагничивание трансформатора DР_х + jDQ_x.

Для трансформатора известны следующие паспортные (каталожные) данные:

S_ном – номинальная мощность, МВ×А;

U_В,ном; U_Н,ном – номинальные линейные напряжения обмоток высшего и низшего напряжений, кВ;

DР_х – активные потери холостого хода, кВт;

I_х,% — ток холостого хода, % I_ном;

DР_к – потери короткого замыкания, кВт;

u_к,% — напряжение короткого замыкания, % U_ном;

Группа соединений обмоток.

По этим данным можно определить все параметры схемы замещения трансформатора (сопротивления и проводимости), а также потери мощности в нем.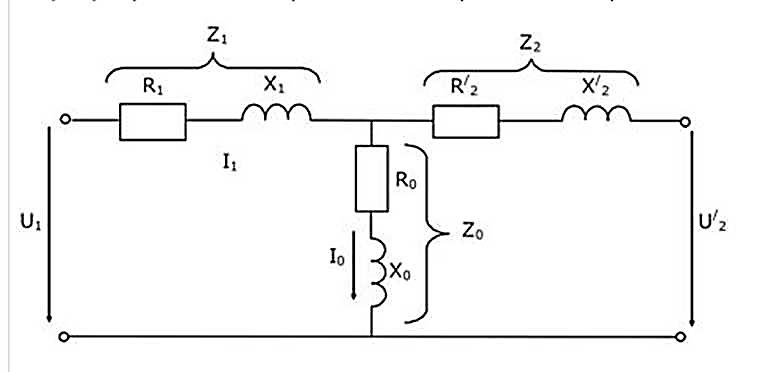

Проводимости ветви намагничивания определяются результатами опыта х.х. В этом режиме трансформатор потребляет лишь мощность, определяемую потерями х.х.,

Проводимости [в сименсах — См] определяются выражениями

, ,

где принято выражать U_ном [кВ]; DР_х[МВт]; DQ_x [МВ×Ар].

Как известно, потери активной мощности в сердечнике трансформатора не зависят от его нагрузки и для данного трансформатора являются постоянными при условии неизменности напряжения, приложенного к первичной обмотке. При номинальном (каталожном) первичном напряжении DР_х постоянна и равна каталожному значению.

Фазовый сдвиг между напряжением, приложенным к первичной обмотке, и током холостого хода стремится к 90⁰, что обуславливает очень малое значение активной составляющей.

Следовательно, можно считать, что

где — реактивная составляющая I_x.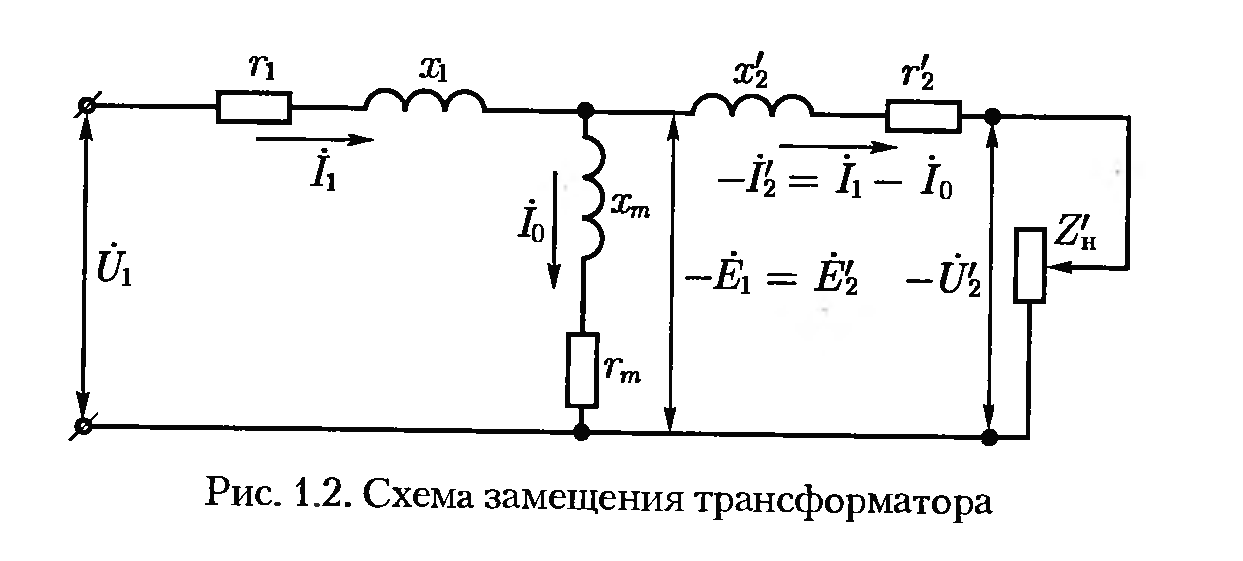

Поэтому

В виду уже отмеченного соотношения между активной и реактивной составляющими тока холостого хода DР_х << DQ_x и потому полная мощность трансформатора S в режиме холостого хода приближенно равна намагничивающей мощности DQ_x.

Проводимость b_т определяется так:

Сопротивления r_т и x_т находят из опыта короткого замыкания. С учетом U_k << U_номпотерями мощности в сердечнике можно пренебречь. Тогда

;

В современных мощных трансформаторах r_т<< x_т и u_к » , где — реактивная составляющая. Из опыта короткого замыкания

Умножая последнее выражение на U_ном, после преобразований получаем

Для получения r_т и x_т в Омах необходимо подстановку мощности выполнять в МВт или МВ×Ар, а подстановку напряжения в кВ.

Потери активной мощности в r_т зависят от тока и мощности нагрузки I₂и S₂ и равны

Подставив в последнее выражение значение r_т и допустив, что , получаем

Это соображение полностью соответствует известному из курса «Электрические машины» выражению . Аналогично потери реактивной мощности в х_т имеют вид

Для трансформатора, через который проходят ток нагрузки I₂ и мощность S₂, потери мощности равны

; (2.20)

. (2.21)

Если на подстанции с суммарной нагрузкой S₂ работают параллельно k одинаковых трансформаторов, то их эквивалентные сопротивления в k раз меньше и равны r_т/k и х_т/k, а проводимости в k раз больше и равны k×g_{т и}k×b_т.

Тогда для k параллельно включенных одинаковых трансформаторов получаем

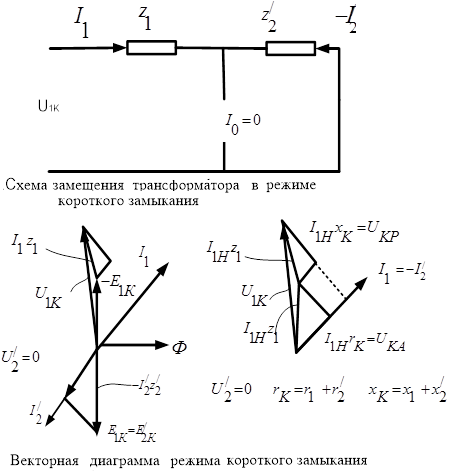; (2. 22)

. (2.23)

Возможно также получение приведенных выражений и другим способом. А именно, если подставить в (2.20) и (2.21) вместо S₂ поток мощности, текущей через каждый трансформатор и равной S₂/k , то получаем потери мощности в одном трансформаторе. Умножим их на k и получим (2.22) и (2.23) для потерь мощности в k параллельно работающих трансформаторах.

Пример 2.1.Определим параметры схемы замещения двухобмоточного трансформатора типа ТМ – 630/10, приведенные к номинальным напряжениям первичной и вторичной обмоток (рис. 2.11)

Рис. 2.11. Двухобмоточный трансформатор:

а — упрощенная схема замещения;

б – Г-образная схема замещения.

В справочной литературе находим каталожные данные трансформатора: S_ном = 630 кВ×А; U_В,ном = 10 кВ; U_Н,ном = 0,4 кВ; DР_к = 8,5 кВт; DР_х = 1,65 кВт; U_к,% = 5,5 %; I_х,% = 3 %.

При подстановке в расчетные соотношения напряжений в киловольтах, а мощностей – в мегавольт-амперах (мегаваттах), значения сопротивлений получим в Омах, а проводимостей — в сименсах. Рассчитаем активные сопротивления трансформатора r_т и , приведенные к номинальным напряжениям первичной обмотки (10 кВ) и вторичной обмотки (0,4 кВ).

Расчетные соотношения будут отличаться друг от друга лишь величиной номинального напряжения

Ом;

Ом.

Рассчитаем индуктивные сопротивления трансформатора

Ом;

Ом.

Активные проводимости намагничивающего контура так же, как и ранее определенные сопротивления, будут рассчитываться различно для приведения их к сторонам высшего и низшего напряжений

См;

См.

Реактивные проводимости намагничивания

См;

См.

Для трансформаторов с U_В,ном £ 220 кВ допустимо использование схемы замещения, где ветвь намагничивания замещена мощностью потерь холостого хода

Потери активной мощности DР_хизвестны из каталожных данных. Потери реактивной мощности DQ_х рассчитываются

МВАр,

тогда МВ×А.

Заметим, что величины r_т и x_т, приведенные к стороне ВН, и DQ_xмогут быть непосредственно взяты их справочных данных.

Упрощенная схема — замещение — трансформатор

Cтраница 1

Упрощенная схема замещения трансформатора может быть получена и другим путем, который и рассмотрим. [2]

Используя упрощенную схему замещения трансформатора, постройте векторную диаграмму для случая, когда ко вторичной обмотке подключен конденсатор большой емкости. [3]

В каких случаях используются упрощенные схемы замещения трансформаторов. [4]

Упрощенная векторная диаграмма соответствует упрощенной схеме замещения трансформатора ( см. рис. 14 — 6), в которой намагничивающий ток принят равным нулю. [6]

В общем случае векторная диаграмма упрощенной схемы замещения трансформатора имеет другой вид. [7]

На рис. 7 — 9 показана несколько упрощенная схема замещения трансформатора при перенапряжениях. [8]

Вторичное напряжение Ич легко выразить через постоянное по величине первичное напряжение Uit рассматривая упрощенную схему замещения трансформатора, представленную на рис 6.16. В этой схеме отсутствует ветвь намагничивания. [9]

Вторичное напряжение U2 можно выразить через постоянное по величине первичное напряжение Ult если рассмотреть упрощенную схему замещения трансформатора, представленную на рис. 6.16. В этой схеме отсутствует ветвь намагничивания. [11]

Для анализа отдельных режимов асинхронного двигателя может быть применена также и упрощенная схема замещения, подобная упрощенной схеме замещения трансформатора, в которой опущена ветвь намагничивания с током / о. [12]

Для анализа отдельных режимов асинхронного двигателя может быть применена также и упрошенная схема замещения, подобная упрощенной схеме замещения трансформатора, в которой опущена ветвь намагничивания с током / о. [13]

Опыт короткого замыкания трансформатора проводится в процессе исследований трансформатора для определения электрических потерь мощности в проводах обмоток и параметров упрощенной схемы замещения трансформатора. [14]

Страницы: 1 2

Схема замещения Трансформатора. Опытное определение параметров схемы замещения

Параметры схемы замещения для любого трансформатора можно определить по данным опытов холостого хода и короткого замыкания (рис. 2.20).

Опыт холостого хода заключается в следующем. К зажимам одной изобмоток посредством регулятора напряжения (РН) (рис. 2.20, а) подводят номинальное напряжение ; к другой обмотке подключают вольтметр (ее можно считать разомкнутой). Измерив ток холостого хода I₀и мощность P₀, потребляемую трансформатором, согласно схеме замещения (рис. 2.21, а) находят

(2.33)

Так как ток холостого хода мал по сравнению с номинальным током трансформатора, электрическими потерями пренебрегают и считают, что вся мощность, потребляемая трансформатором, расходуется на компенсацию магнитных потерь в стали магнитопровода. При этом

откуда

Рис. 2.21. Схема замещения трансформатора (а) и его векторные диаграммы (б, в) для режима холостого хода

Аналогично считают, что X₁+X_m≈X_m, так как сопротивление Х_топределяется основным потоком трансформатора Ф (потоком взаимоиндукции), a X₁ — потоком рассеяния Ф_σ1, который во много раз меньше Ф. Поэтому с большой степенью точности полагают, что

Измерив напряжения U₀ и U₂₀ первичной и вторичной обмоток, определяют коэффициент трансформации

(2.36)

Векторная диаграмма трансформатора в режиме холостого хода, построенная исходя из указанных выше допущений, изображена на рис. 2.21, б. В действительности ток /₀ создает в первичной обмотке падения напряжения jI₀X₁ поэтому Соответствующая векторная диаграмма показана на рис. 2.21, в, однако падения напряжения там показаны увеличенными, так как они составляют доли процента и при соблюдении масштаба были бы не заметны.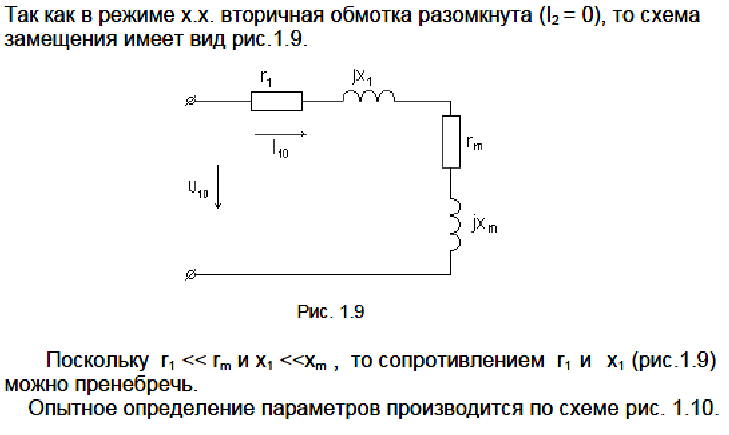

Рис. 2.22. Схема замещения трансформатора {а) и его векторная диаграмма {б) для режима короткого замыкания

Опыт короткого замыкания характеризуется тем, что вторичную обмотку замыкают накоротко (сопротивление Z_H=0), а к первичной посредством регулятора напряжения РН подводят пониженное напряжение U_к(см.рис. 2.20, б) такого значения, при котором по обмоткам проходит номинальный ток I_ном. В мощных силовых трансформаторах напряжение U_кпри коротком замыкании обычно составляет 5-15% от номинального. В трансформаторах малой мощности напряжение U_к может достигать 25-50% от U_ном.

Так как поток, замыкающийся по стальному магнитопроводу, зависит от напряжения, приложенного к первичной обмотке трансформатора, а магнитные потери в стали пропорциональны квадрату индукции, т. е. квадрату магнитного потока, то ввиду малости U_к пренебрегают магнитными потерями в стали и током холостого хода.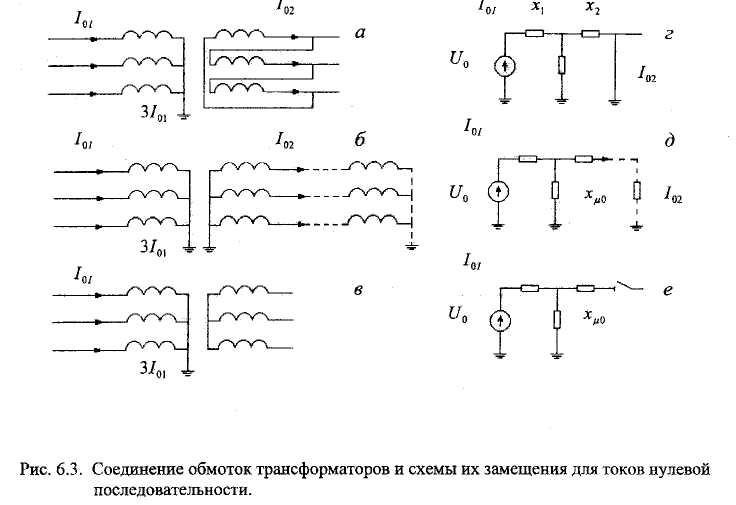 При этом из общей схемы замещения трансформатора исключают сопротивления R_m и Х_т и преобразуют ее в схему, показанную на рис. 2.22, а. Параметры этой схемы определяют из следующих соотношений:

Разделить Z_к на составляющие Z₁ и Z₂ довольно трудно. Обычно принимают схему замещения симметричной, полагая Z₁= Z’₂ = 0,5Z_к. Это допущение близко к действительности и не вносит ощутимых погрешностей в расчеты. Векторная диаграмма трансформатора при коротком замыкании показана на рис. 2.22, б.

Треугольник ABC, образуемый векторами активного, реактивного и полного падений напряжения, называют треугольником короткого замыкания или характеристическим треугольником.

При изменении режима работы трансформатора (тока нагрузки) катеты характеристического треугольника изменяются пропорционально изменению тока. Это позволяет, как показано ниже, очень просто перестраивать векторные диаграммы для упрощенной схемы замещения трансформатора и производить количественные расчеты. Катеты ВС и АС называют соответственно реактивной и активной составляющими напряжения короткого замыкания. В ГОСТ ах и паспортах трансформаторов указывают относительное напряжение короткого замыкания при номинальном токе в процентах от номинального напряжения:

Аналогично можно выразить относительные значения его активной и реактивной составляющих (в %):

(2.39)

При этом

При расчете параметров трансформатора по (2.37) не имеет значения, на какой из обмоток проводится опыт короткого замыкания. Его удобнее проводить при замыкании накоротко обмотки с меньшим числом витков, но вообще следует исходить из удобства подбора приборов и обеспечения условий техники безопасности. По известному значению и_к% можно определить установившийся ток короткого замыкания в реальных условиях эксплуатации (при номинальном напряжении):

(2.41)Обычно в силовых трансформаторах большой и средней мощности значение и_к% составляет 5-15%. Поэтому ток короткого замыкания в них в 7-20 раз превышает номинальный. Как правило, чем больше мощность и напряжение силового трансформатора, тем выше напряжение короткого замыкания и_к%.

Что такое эквивалентная схема трансформатора?

— Объявление —

Equivalent Circuit of Transformer — это электрическая схема, объясняющая уравнения, представляющие поведение этого трансформатора. Фактически, эквивалентная схема любого электрического прибора важна для анализа его работы и выявления любых возможностей дальнейшего изменения моделирования. Эквивалентная схема трансформатора включает в себя настройку индуктивности, сопротивления, напряжения, емкости и т. Д.Затем эти схемы можно анализировать и исследовать, применяя принципы теории диаграмм.

Какая эквивалентная схема трансформатора?

Эквивалентная схема или диаграмма любой системы может быть относительно полезной для предварительного определения характеристик прибора в различных ситуациях различных операций. Он может легко представить поведение схемы с помощью конкретного уравнения, полностью описывающего состояние системы.

Например, эквивалентный импеданс системы жизненно важен для оценки, поскольку трансформатор является электрическим силовым инструментом для рассмотрения нескольких характеристик электрического силового устройства, которые могут потребоваться для оценки всего внутреннего импеданса трансформатора в системе электроснабжения. , исследование с первичной или вторичной стороны в зависимости от требований.

Эта оценка фактически требует эквивалентной схемы трансформатора на основе основной стороны эквивалентной схемы трансформатора и вторичной стороны соответственно. Относительный импеданс также является очень важной характеристикой трансформатора. Посетите здесь, чтобы увидеть важность этого расчета при проектировании любой схемы.

Представлена упрощенная эквивалентная схема трансформатора с учетом всех свойств трансформатора на первичной или вторичной стороне.Основная эквивалентная схема трансформатора показана ниже на схеме:

Эквивалентная схема трансформатора (Ссылка: circuitglobe. com )

Этой особенности следует уделять большое внимание при установке трансформатора в существующий система электроснабжения. Относительный импеданс различных силовых трансформаторов должен быть полностью согласован на основе параллельной конфигурации энергосистем. Относительный импеданс может быть извлечен из эквивалентного значения импеданса трансформатора, поэтому можно заметить, что эквивалентная схема трансформатора также важна при оценке относительного импеданса.

Мы можем определить эквивалентную схему трансформатора на основе коэффициента трансформации как:

K = \ frac {{E} _ {2}} {{E} _ {1}}

Где E ₁ — наведенная ЭДС, равная используемому основному напряжению (В ₁) с небольшим уменьшением напряжения. Это напряжение влияет на систему, вырабатывая ток I ₀ или ток холостого хода в первой обмотке трансформатора. Величина тока холостого хода слишком мала, поэтому в расчетах им можно пренебречь.

В первую очередь мы должны установить общие правила в системе для управления эквивалентной схемой трансформатора, затем мы можем изменить ее для подготовки к определению правил на основе первичной обмотки. Для этого, во-первых, нам необходимо представить полную векторную диаграмму трансформатора, которая представлена на рисунке ниже.

Векторная диаграмма трансформатора (Ссылка: lectric4u.com )

В результате I ₁ = I ’₁. Далее ток холостого хода разделен на две части: намагниченный ток (I _m) и рабочий ток (I _w).{‘}} {K} = \ frac {{I} _ {1} — {I} _ {0}} {K}

Напряжение подключения V ₂ внутри нагрузки такое же, как и конкретная ЭДС E ₂ в следующей обмотке с небольшим понижением напряжения во второй обмотке.

Эквивалентная схема трансформатора, когда все величины относятся к первичной стороне

В этом методе для получения эквивалентной схемы трансформатора все характеристики должны рассматриваться как первичная часть, как показано на рисунке ниже:

Эквивалентная цепь трансформатора, относящаяся к первичной стороне (Ссылка: circuitglobe. {‘}
Примерная эквивалентная схема трансформатора
Из-за небольшого значения I ₀ по сравнению с I ₁, оно составляет менее 4 процентов от общей нагрузки первичного тока и изменяет снижение напряжения незначительно. В результате это идеальное приближение для уменьшения эффекта возбуждения схемы в приближенной эквивалентной схеме трансформаторного метода. Сопротивление и реактивное сопротивление обмотки расположены в последовательной конфигурации, которая теперь может быть введена как эквивалентное реактивное сопротивление и сопротивление трансформатора для любой конкретной стороны.{‘} = K {V} _ {2}
Примерная эквивалентная цепь трансформатора, относящаяся к первичной стороне (Ссылка: lectric4u.com )
Эквивалентная цепь трансформатора, когда все величины относятся к вторичной стороне
Эквивалентная схема трансформатора или базовая схема представлена ниже, когда все функции спроектированы на основе вторичной обмотки.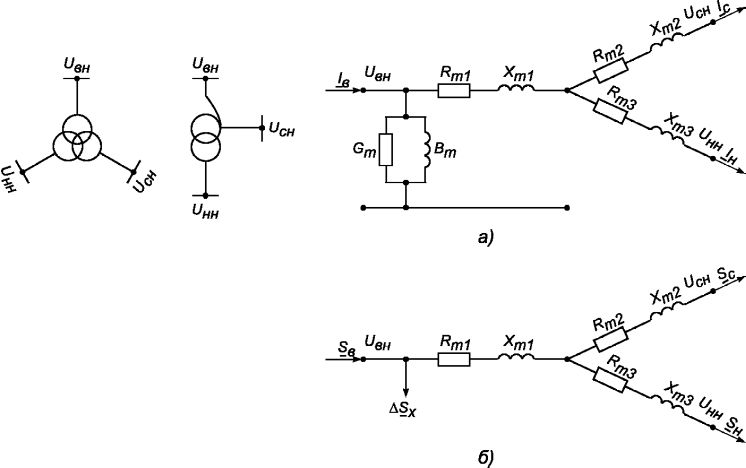 Эквивалентная цепь
, относящаяся к вторичной стороне (Ссылка: circuitglobe.com )
Следующие свойства представляют собой значения сопротивления и реактивного сопротивления, которые можно получить ниже.{‘}
Поскольку ток холостого хода или I ₀ обычно составляет от 2 до 4 процентов от значения полной нагрузки номинального тока, параллельная конфигурация включает сопротивление R ₀, а реактивное сопротивление X ₀ может быть удаляется из схемы без внесения какой-либо конкретной ошибки в работу трансформатора при приложении нагрузки.
Мы также можем применить дальнейшее упрощение в эквивалентной схеме трансформатора, удалив параллельные члены в схеме, включая R ₀ и X ₀.Эта упрощенная схема системы представлена ниже:
Упрощенная эквивалентная схема трансформатора (Ссылка: circuitglobe.com )
Это все существенные проблемы, связанные с эквивалентной схемой трансформатора.
— Объявление —
Схема замещения трансформатора | electricaleasy.com
В практичном трансформере —
(a) Некоторый поток утечки присутствует как на первичной, так и на вторичной стороне. Эта утечка приводит к возникновению реактивных сопротивлений утечки с обеих сторон, которые обозначаются как X ₁ и X ₂ соответственно.
(b) И первичная, и вторичная обмотки обладают сопротивлением, обозначенным как R ₁ и R ₂ соответственно. Эти сопротивления вызывают падение напряжения, как I ₁ R ₁ и I ₂ R ₂, а также потери в меди I ₁ ² R ₁ и I ₂ ² R ₂.
(c) Проницаемость сердечника не может быть бесконечной, поэтому необходим некоторый ток намагничивания. Взаимный поток также вызывает потери в сердечнике в железных частях трансформатора.
Чтобы вывести эквивалентную схему трансформатора , необходимо учесть все вышеперечисленное.
Эквивалентная схема трансформатора Сопротивления и реактивные сопротивления трансформатора, описанные выше, можно представить отдельно от обмоток (как показано на рисунке ниже). Следовательно, функция обмоток в дальнейшем будет только преобразовывать напряжение.
Ток холостого хода I ₀ делится на чистую индуктивность X ₀ (принимая компоненты намагничивания I _μ) и неиндукционное сопротивление R ₀ (принимая рабочий компонент I _w), которые соединены параллельно через Главная.Значение E ₁ может быть получено путем вычитания I ₁ Z ₁ из V ₁. Значение R ₀ и X ₀ можно рассчитать как, R ₀ = E ₁ / I _w и X ₀ = E ₁ / I _μ.
Но использование этой эквивалентной схемы не упрощает вычислений. Чтобы упростить вычисления, предпочтительно передавать ток, напряжение и полное сопротивление либо на первичную, либо на вторичную стороны. В этом случае придется работать только с одной обмоткой, что удобнее.
Из коэффициента трансформации напряжения видно, что
E ₁ / E ₂ = N ₁ / N ₂ = K
Теперь давайте отнесем параметры вторичной стороны к первичной.
Z ₂ может называться первичным как Z ₂ ‘
, где Z ₂‘ = (N ₁ / N ₂) ² Z ₂ = K ² Z ₂…………. где K = N ₁ / N ₂.
, то есть R ₂ ‘+ jX ₂‘ = K ² (R ₂ + jX ₂)
приравнивание действительной и мнимой частей,
R ₂ ‘= K ² R ₂ и X ₂ ‘= K ² X ₂.
А В ₂ ‘= КВ ₂
На следующем рисунке показана эквивалентная схема трансформатора с вторичными параметрами, относящимися к первичному .

Теперь, когда значения сопротивления обмотки и реактивного сопротивления утечки настолько малы, что V ₁ и E ₁ можно считать равными. Следовательно, возбуждающий ток, потребляемый параллельной комбинацией R ₀ и X ₀, не повлияет существенно, если мы переместим его на входные клеммы, как показано на рисунке ниже.

Теперь пусть R ₁ + R ₂ ‘= R’eq и X ₁ + X ₂‘ = X’eq
Тогда эквивалентная схема трансформатора станет такой, как показано на рисунке ниже
Примерная схема замещения трансформатора
Если рассчитывается только регулировка напряжения, то можно пренебречь даже всей ветвью возбуждения (параллельная комбинация R0 и X0).Тогда эквивалентная схема станет такой, как показано на рисунке ниже
.
Эквивалентная принципиальная схема однофазного трансформатора
| Electricalunits.com

Эквивалентная принципиальная схема трансформатора — это, по сути, схема, которая может быть преобразована в эквивалентную схему, в которой сопротивление и реактивное сопротивление рассеяния трансформатора считаются внешними по отношению к обмотке.
Эквивалентная схема трансформатора приведена ниже: —
Где, R ₁ = Сопротивление первичной обмотки.R ₂ = Сопротивление вторичной обмотки. I ₀ = Ток холостого хода. I _µ = намагничивающий компонент, I _w = Рабочий компонент, Эти I _µ и I _w подключены параллельно через первичный контур. Значение E ₁ (первичная ЭДС) получается векторным вычитанием I ₁ Z ₁ из V ₁. Значение X ₀ = E ₁ / I ₀ и R ₀ = E ₁ / I _w.Мы знаем, что отношение E ₁ и E ₂ составляет E ₂ / E ₁ = N ₂ / N ₁ = K, (коэффициент трансформации)
Используя эквивалентную схему, мы можем легко вычислить полное сопротивление передачи напряжения, тока и полного сопротивления первичной или вторичной обмотке.
Вторичная цепь показана на рис-1. и его эквивалентное первичное значение показано на рис. 2,
рис-1
рис-2
Полная эквивалентная схема трансформатора получается добавлением полного сопротивления первичной обмотки, как показано на — Рис-3.
рис-3
И можно упростить клеммы, показанные на рис. 4, и еще более упростить эквивалентную схему, показанную на рис. 5,
.
рис-4
Наконец, схема упрощена за счет полного исключения I ₀, как показано на рис. 5.
рис-5
По эквивалентной схеме, показанной на рис. 3, полное сопротивление между входными клеммами равно
.
Это так, потому что есть две параллельные цепи, одна с импедансом Z _м, а другая с Z ’₂ и Z’ _L, включенными последовательно друг с другом.
Подробная информация: —
electric4u. com

Недавнее сообщение
Вопрос с множественным выбором (MCQ) батареи стр.-19: 181. Алюминий производится из бокситов на А) пенная флотация Б) вращающийся В) окисление Г) электролитический процесс.
Подробнее …
Вопрос с множественным выбором (MCQ) батареи стр.-18: 171.Самая низкая плотность тока обычно рекомендуется для покрытия А) хром Б) серебро В) бронза Г) кадмий.
Подробнее …
Вопрос с множественным выбором (MCQ) батареи стр.-17: 161. Выберите правильное соотношение A) Изменение = потенциал / мощность Б) Потенциал = Заряд / емкость C) Емкость = потенциал × заряд D) Потенциал = Заряд × емкость.
Подробнее …
Схема, эквивалентная
трансформатора? Обращается к первичной и вторичной стороне
Эквивалентная принципиальная схема любого устройства может быть весьма полезна для предварительного определения поведения устройства в различных условиях эксплуатации. Это просто схематическое представление уравнения, описывающего производительность устройства.
Нарисована упрощенная эквивалентная схема трансформатора, представляющая все параметры трансформатора либо на вторичной, либо на первичной стороне. Эквивалентная принципиальная схема трансформатора приведена ниже:
ЭКВИВАЛЕНТНАЯ СХЕМА ТРАНСФОРМАТОРА
Состав:
Пусть эквивалентная схема трансформатора с коэффициентом трансформации K = E ₂ / E ₁
Индуцированная ЭДС E ₁ равна приложенному первичному напряжению V ₁ за вычетом падения первичного напряжения.Это напряжение вызывает ток I ₀ холостого хода в первичной обмотке трансформатора. Значение тока холостого хода очень мало, поэтому им пренебрегают.
Следовательно, I ₁ = I ₁ ’. Ток холостого хода далее делится на две составляющие, называемые током намагничивания (I _m) и рабочим током (I _w).
Эти две составляющие тока холостого хода обусловлены током, потребляемым неиндуктивным сопротивлением R ₀ и чистым реактивным сопротивлением X ₀, имеющим напряжение E ₁ или (V ₁ — падение первичного напряжения).
Вторичный ток I ₂ равен
Напряжение на зажимах V ₂ на нагрузке равно наведенной ЭДС E ₂ во вторичной обмотке за вычетом падения напряжения во вторичной обмотке.
Эквивалентный контур, когда все количества относятся к первичной стороне
В этом случае, чтобы нарисовать эквивалентную схему трансформатора, все величины должны быть отнесены к первичной обмотке, как показано на рисунке ниже:
Принципиальная схема трансформатора, когда все вторичные величины относятся к первичной стороне
Ниже приведены значения сопротивления и реактивного сопротивления, указанные ниже
.
Сопротивление вторичной обмотки относительно первичной обмотки равно:
Эквивалентное сопротивление первичной обмотки:
Вторичное реактивное сопротивление относительно первичной стороны определяется как:
Эквивалентное реактивное сопротивление первичной обмотки определяется как:

Эквивалентная цепь, когда все количества относятся к вторичной стороне
Эквивалентная принципиальная схема трансформатора показана ниже, когда все величины относятся к вторичной обмотке.
Принципиальная схема трансформатора, когда все первичные величины относятся к вторичной стороне
Ниже приведены значения сопротивления и реактивного сопротивления, указанные ниже
.
Первичное сопротивление, относящееся к вторичной стороне, определяется как
Эквивалентное сопротивление вторичной обмотки составляет
.
Первичное реактивное сопротивление относительно вторичной стороны равно
.
Эквивалентное реактивное сопротивление вторичной обмотки равно
.
Ток холостого хода I ₀ вряд ли от 3 до 5% номинального тока при полной нагрузке, параллельная ветвь, состоящая из сопротивления R ₀ и реактивного сопротивления X ₀, может быть опущена без внесения каких-либо заметных ошибок в поведение трансформатора в нагруженном состоянии.
Дальнейшее упрощение эквивалентной схемы трансформатора можно сделать, пренебрегая параллельной ветвью, состоящей из R ₀ и X ₀.
Упрощенная принципиальная схема трансформатора представлена ниже:
Упрощенная схема эквивалента трансформатора
Это все об эквивалентной схеме трансформатора.
Эквивалентная схема и фазовая схема трансформатора
Чтобы понять эквивалентную схему трансформатора, мы предлагаем вам сначала прочитать Идеальный трансформатор , а затем вернуться и продолжить с этого места.
Что такое эквивалентная схема трансформатора?
Эквивалентная схема трансформатора — это схематическое изображение практического трансформатора, которое показывает все электрические параметры, такие как сопротивление обмотки, реактивное сопротивление, проводимость, проводимость, первичные и вторичные напряжения, токи и т. Д. Теперь давайте погрузимся в тему и прежде всего , давайте познакомимся с реальным трансформатором.
На рисунке показан реальный трансформатор с нагрузкой, подключенной к его вторичной обмотке.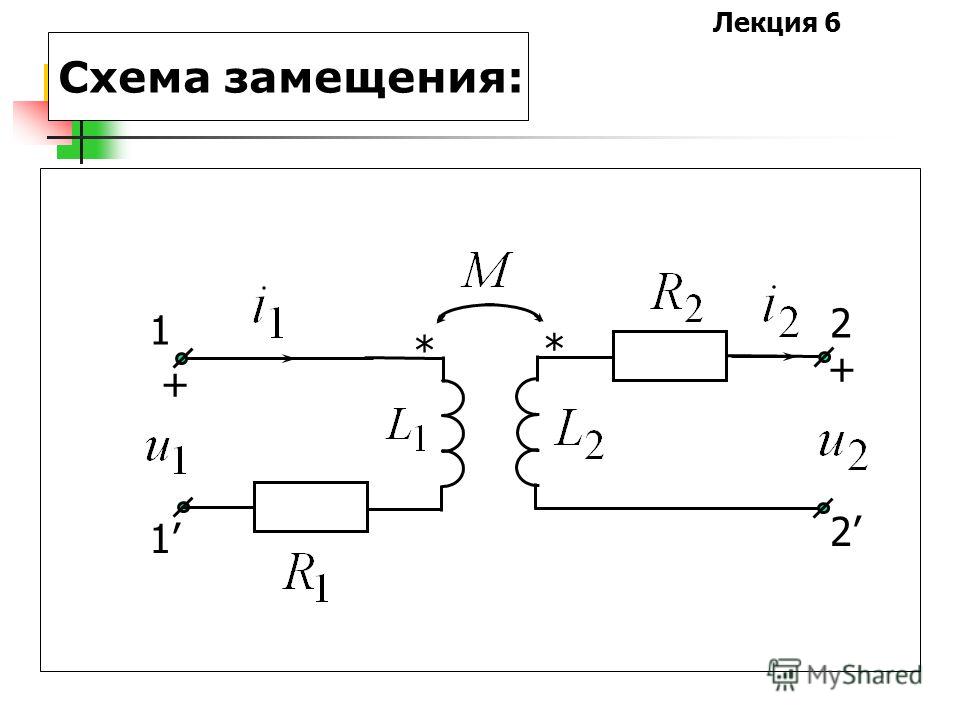 Как вы знаете, первичный и вторичный проводники имеют конечное сопротивление.
Пусть R ₁ будет сопротивлением первичной обмотки, а R ₂ будет сопротивлением вторичной обмотки. Когда через эти катушки протекает ток, определенная мощность теряется из-за ее омического сопротивления. Поскольку проводник сделан из меди, потеря мощности также известна как потери в меди.
Считаем, что трансформатор имеет N ₁ количество витков первичной обмотки и N ₂ количество витков вторичной обмотки.V ₁ — напряжение, приложенное к первичной катушке, которое индуцирует ЭДС E ₁ в первичной катушке и E ₂ во вторичной катушке.
Импеданс нагрузки Z добавляется к клеммам вторичной обмотки, так что он стекает ток I ₂ из вторичной обмотки трансформатора, который пропорционален I ₁ на первичной обмотке трансформатора. Пусть V ₂ будет напряжением, измеренным на нагрузке.
Большая часть потока Φ связывает первичную и вторичную обмотки и ограничена сердечником, в то время как небольшая часть этого потока просачивается в окружающий воздух.Пусть Φ _PL и Φ _SL будут потоками рассеяния, связывающими первичную и вторичную обмотки соответственно.
Первичная и вторичная катушки обладают сопротивлением (R ₁ и R ₂) и реактивным сопротивлением (X _l1 и X _l2) и оказывают последовательное воздействие на обмотку.
В дополнение ко всему вышесказанному, существует ток намагничивания и составляющая тока потерь в сердечнике, которые обозначены I _m и I _i соответственно.Как известно, коэффициент трансформации мощности трансформатора равен
.
Падение напряжения из-за сопротивления и реактивного сопротивления утечки слишком мало, так что
Схема замещения трансформатора
Надеюсь, вы поняли все сделанные предположения и соображения.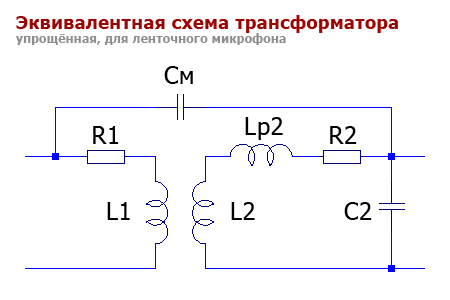 Теперь пора нарисовать эквивалентную схему трансформатора.
Как было сказано ранее, трансформаторы потребляют ток возбуждения Io, имеющий намагничивающую составляющую I _m, которая генерирует магнитный поток Φ и составляющую потерь в сердечнике I _i.Со всеми вышеперечисленными деталями можно построить схемную модель реального трансформатора.
Рисунок (a)
Где G _i и B _m представляют потери в сердечнике и составляющую намагниченности соответственно.
Как обсуждалось в разделе «Идеальный трансформатор», вторичное сопротивление и реактивное сопротивление могут быть отнесены к первичной стороне следующим образом:
Аналогично
Рисунок (b)
Рисунок (b) показывает результирующую схему.
После привязки импедансов, напряжения и тока к первичной обмотке представление сердечника больше не требуется. Следовательно, схема может быть уменьшена до Т-образной схемы, как на рисунке (C).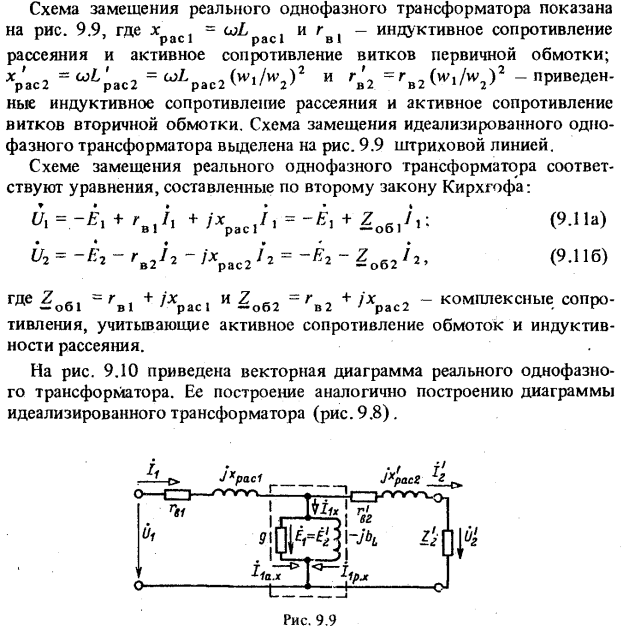
Рисунок (c)
Точно так же эквивалентную схему можно отнести к вторичной, преобразовав импеданс и полную проводимость первичной обмотки во вторичную, умножив их на квадрат отношения витков.
Рисунок (d)
Фазорная схема трансформатора
Можно нарисовать векторную диаграмму трансформатора со ссылкой на эквивалентную схему трансформатора.
Применение закона Кирхгофа о напряжении к фигуре
Фактическая векторная диаграмма трансформатора Эквивалентная схема трансформатора
— ваше руководство по электрике

Эквивалентная схема трансформатора показана на рисунке.

Компоненты без нагрузки

Первичный ток холостого хода I _o имеет две составляющие, а именно I _m и I _w.

Где I _м = намагничивающая составляющая = I _o sin φ _o
и I _w = компонент потерь в сердечнике = I _o cos φ _o.
I _w обеспечивает потери холостого хода и, как предполагается, протекает через сопротивление холостого хода, которое также известно как сопротивление потерь в сердечнике (R _или).
Предполагается, что намагничивающая составляющая I _м протекает через реактивное сопротивление, известное как реактивное сопротивление намагничивания, X _o.
Параллельная комбинация R _o и X _o также известна как схема возбуждения .
Из эквивалентной схемы трансформатора ,

R _o = V ₁/ I _w и X _o = V ₁/ I _m.
Основные компоненты
Сопротивление R ₁ и реактивное сопротивление X ₁ соответствуют сопротивлению обмотки (сопротивлению постоянному току) и реактивному сопротивлению утечки первичной обмотки.
Полный ток I ₁ на первичной стороне равен векторной сумме I _o и I ₂ ’.
I ₂ ’= K I ² — дополнительный первичный ток, протекающий из-за нагрузки, подключенной на вторичной стороне трансформатора.
Вторичные компоненты
Сопротивление R ₂ и реактивное сопротивление X ₂ соответствуют сопротивлению обмотки и реактивному сопротивлению утечки вторичной обмотки.
Сопротивление нагрузки Z _L может быть резистивным, индуктивным или емкостным.
Эквивалентная схема однофазного трансформатора дополнительно упрощена путем переноса всех величин либо на первичную, либо на вторичную сторону.
Это сделано для упрощения расчетов.
Эквивалентная цепь трансформатора относительно первичной

Все компоненты вторичной обмотки трансформатора перенесены на первичную обмотку, как показано на рисунке.
R ₂ ’, X ₂’ и Z _L ’являются значениями R ₂, X ₂ и Z _L, относящимися к первичным соответственно.
Значения этих компонентов получаются следующим образом:

R ₂ ‘= R ₂ / K ², X ₂‘ = X ₂ / K ² и Z _L ‘= Z _L / K ²

где K = N ₂ / N ₁ (коэффициент трансформации).
Эквивалентная цепь трансформатора, относящаяся к вторичной обмотке

Эквивалентная схема трансформатора , относящаяся к вторичной стороне, показана на рисунке.
Компоненты R ₁ ’, X ₁’, R _o ’и X _o’ являются первичными компонентами, относящимися к вторичным. Выражения для этих компонентов следующие:

R ₁ ‘= K ² R ₁, X ₁‘ = K ² X ₁

R _o ‘= K ² R _o, X _o ‘= K ² X _o
Первичные напряжения и токи также передаются на вторичную сторону как I ₁‘, V ₁ ‘, I _o ‘, E ₁‘ соответственно и даются по:

I ₁ ‘= I ₁ / K, E ₁‘ = KE ₁, I _o ‘= I 900 o / K

, где K = N ₂ / N ₁ (коэффициент трансформации).

Примерная эквивалентная схема — это схема, которая получается путем смещения схемы возбуждения влево от R ₁ и X ₁, как показано на рисунке.

Хотя это смещение создает ошибку в падении напряжения на R ₁ и X ₁, но оно значительно упрощает работу по расчету и дает значительно упрощенную эквивалентную схему.

Трансформатор | Все сообщения
© https: // yourelectricalguide.ком / схема замещения трансформатора.
Эквивалентная схема трансформатора
, относящаяся к первичной и вторичной стороне
Все трансформаторы имеют сопротивление обмотки, сердечник с конечной магнитной проницаемостью, потоком утечки, гистерезисом и потерями на вихревые токи и поэтому не идеальны. Их можно представить в виде эквивалентной схемы, которая позволяет нам анализировать трансформатор.
Характеристики неидеального трансформатора
Неидеальный трансформатор показан на рис. 1. Его можно описать следующими характеристиками:
1. Имеется утечка магнитного потока, что означает, что не весь магнитный поток, создаваемый одной обмоткой, будет связывать другую обмотку.
2. Первичная и вторичная обмотки имеют сопротивления, что означает, что приложенное напряжение (напряжение источника) v ₁ НЕ совпадает с наведенным первичным напряжением e ₁; то есть v ₁ ≠ e ₁. Аналогично v ₂ ≠ e ₂.
3.Магнитный сердечник НЕ обладает идеальной проницаемостью, что означает, что для его намагничивания требуется конечная ммс.
4. Поскольку поток в магнитопроводе переменный, существуют гистерезисные, а также потери на вихревые токи, которые в совокупности называются потерями в сердечнике или железе.
Эквивалентная схема трансформатора
При выводе эквивалентной схемы для двухобмоточного трансформатора, показанного на рисунке 1, необходимо смоделировать характеристики реального трансформатора, описанные ранее.
Рассмотрим первичный контур. Уравнение напряжения вокруг контура можно записать как
\ [\ begin {matrix} {{\ nu} _ {1}} = {{R} _ {1}} {{i} _ {1}} + { {N} _ {1}} \ frac {d {{\ lambda} _ {1}}} {dt} = {{R} _ {1}} {{i} _ {1}} + {{N} _ {1}} \ frac {d {{\ phi} _ {1}}} {dt} & {} & (1) \\\ end {matrix} \]
Были
R ₁ = Сопротивление первичной обмотки
N ₁ = количество витков первичной обмотки
Поток первичной обмотки ϕ ₁ может быть выражен как сумма взаимного потока ϕ _м и потока утечки первичной обмотки ϕ ₁₁:
$ \ begin {matrix} {{\ phi} _ {1}} = {{\ phi} _ {m}} + {{\ phi} _ {11}} & {} & (2) \\\ конец {матрица} $
Рис.1: Фактический трансформатор
Таким образом, уравнение (1) сводится к
\ [\ begin {matrix} {{\ nu} _ {1}} = {{R} _ {1}} {{i} _ { 1}} + {{N} _ {1}} \ frac {d {{\ phi} _ {11}}} {dt} + {{N} _ {1}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & (3) \\\ end {matrix} \]
Поскольку поток утечки является линейной функцией первичного тока i ₁, второй член справа -сторонняя часть уравнения (3) может быть выражена через индуктивность первичной обмотки. Таким образом,
\ [\ begin {matrix} {{\ nu} _ {1}} = {{R} _ {1}} {{i} _ {1}} + {{L} _ {1}} \ frac {d {{i} _ {1}}} {dt} + {{N} _ {1}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & ( 4) \\\ end {matrix} \]
Далее рассматривается вторичная цепь.Из рис. 1 уравнение напряжения во вторичной обмотке можно записать следующим образом:
\ [\ begin {matrix} {{\ nu} _ {2}} = — {{R} _ {2}} {{i } _ {2}} + {{N} _ {2}} \ frac {d {{\ lambda} _ {2}}} {dt} = — {{R} _ {2}} {{i} _ {2}} + {{N} _ {2}} \ frac {d {{\ phi} _ {2}}} {dt} & {} & (5) \\\ end {matrix} \]
С точки зрения направления потока вторичный поток может быть представлен разницей между взаимным потоком и вторичным потоком утечки:
\ [\ begin {matrix} {{\ phi} _ {2}} = {{\ phi} _ {m}} — {{\ phi} _ {12}} & {} & (6) \\\ end {matrix} \]
Подставляя уравнение (6) в (5), получаем
\ [\ begin { матрица} {{\ nu} _ {2}} = — {{R} _ {2}} {{i} _ {2}} — {{N} _ {2}} \ frac {d {{\ phi } _ {12}}} {dt} + {{N} _ {2}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & (7) \\\ end { matrix} \]
Точно так же поток утечки является линейной функцией вторичного тока i ₂ . Таким образом, уравнение (7) может быть записано с использованием индуктивности вторичной обмотки как:
\ [\ begin {matrix} {{\ nu} _ {2}} = — {{R} _ {2}} {{{ i} _ {2}} — {{L} _ {2}} \ frac {d {{i} _ {2}}} {dt} + {{N} _ {2}} \ frac {d {{ \ phi} _ {m}}} {dt} & {} & \ left (8 \ right) \\\ end {matrix} \]
В уравнениях (4) и (8) последние члены представляют индуцированные напряжения на первичной и вторичной обмотках соответственно; то есть
\ [\ begin {matrix} {{e} _ {1}} = {{N} _ {1}} \ frac {d {{\ phi} _ {m}}} {dt} & {} & \ left (9 \ right) \\\ end {matrix} \]
\ [\ begin {matrix} {{e} _ {2}} = {{N} _ {2}} \ frac { d {{\ phi} _ {m}}} {dt} & {} & \ left (10 \ right) \\\ end {matrix} \]
Разделив уравнение (9) на (10), получим отношение напряжений :
\ [\ begin {matrix} \ frac {{{e} _ {1}}} {{{e} _ {2}}} = \ frac {{{N} _ {1}}} {{ {N} _ {2}}} = a & {} & \ left (11 \ right) \\\ end {matrix} \]
На рис. 2 показана эквивалентная схема двухобмоточного трансформатора, показанного на рис. 1. Элементы схемы, которые используются для моделирования намагниченности сердечника и потерь в сердечнике, могут быть добавлены либо к первичной, либо к вторичной стороне. На рисунке 2 катушка индуктивности L _m1, представляющая намагниченность сердечника, и резистор R _c1, представляющий потери в сердечнике (гистерезис и потери на вихревые токи), подключены параллельно и расположены на первичной стороне эквивалентной схемы трансформатора.
Связанные с сердечником элементы схемы R _c1 и L _m1 обычно определяются при номинальном напряжении и относятся к первичной стороне на рис.2. Предполагается, что они остаются практически постоянными, когда трансформатор работает в номинальных или близких к ним условиях.
Эквивалентная схема трансформатора в векторной форме
В векторной форме эквивалентная схема трансформатора принимает форму, показанную на рисунке 3. Реактивные сопротивления вычисляются путем умножения индуктивностей на радианную частоту $ \ omega = 2 \ pi f $, где f — частота. Отношение витков a = N ₁ / N ₂ приблизительно равно соотношению напряжений V ₁ / V ₂, отношению номинального первичного напряжения к номинальному вторичному напряжению, предоставленному производителем.
Рис. 2: Эквивалентная схема трансформатора
Рис. 3: Эквивалентная схема трансформатора в векторной форме
Векторная диаграмма для нагрузки с отстающим коэффициентом мощности (индуктивной), подключенной ко вторичной обмотке трансформатора на Рис. показан на рис.4.
Используется следующая запись:
\ [\ begin {array} {* {35} {l}} {{\ text {E}} _ {\ text {1}}} = \ text {} primary \ text {} индуцированное \ text {} напряжение \\ {{\ text {E}} _ {\ text {2}}} = \ text {} вторичное \ text {} индуцированное \ text {} напряжение \\ {{\ text {V}} _ {\ text {1}}} = \ text {} первичный \ text {} терминал \ text {} напряжение ~~~~~~~~~~~~~~~~~ \\ { {\ text {V}} _ {\ text {2}}} = \ text {} вторичный \ text {} терминал, \ text {} напряжение \\ \ begin {align} & {{\ text {I}} _ {\ text {1}}} = ~ основной \ text {} текущий \\ & {{\ text {I}} _ {\ text {1}}} = ~ Дополнительный \ text {} текущий \\\ end {align } \\ {{\ text {I}} _ {\ text {e}}} = \ text {} возбуждение \ text {} текущий \\ {{\ text {I}} _ {\ text {m}}} , \ text {} {{X} _ {m}} = \ text {} намагничивание \ text {} текущее \ text {} и \ text {} реактивное сопротивление \\ {{\ text {I}} _ {\ text { c}}}, \ text {} {{R} _ {c}} = \ text {} current \ text {} и \ text {} сопротивление \ text {}, представляющие \ text {} core \ text {} loss \ \ ~~~ {{R} _ {1}} = \ text {} сопротивление \ text {} of \ text {} \ text {} первичная \ text {} обмотка \\ ~~~~ {{R} _ {2}} = \ text {} сопротивление \ text {} из \ t ext {} \ text {} вторичная \ text {} обмотка \\ ~~~~ {{X} _ {1}} = \ text {} первичная \ text {} утечка \ text {} реактивное сопротивление \\ ~~~ ~ {{X} _ {2}} = \ text {} secondary \ text {} Leakage \ text {} Реактивное сопротивление \\\ end {array} \]
Эквивалентная схема трансформатора
, относящаяся к первичной и вторичной сторонам
В схеме замещения трансформатора на рис. 3, идеальный трансформатор можно переместить вправо или влево от эквивалентной схемы, если отнести все величины к первичной или вторичной обмотке, соответственно, как показано на рисунке 5. Это почти всегда делается из-за большой простоты, которую он привносит в анализ трансформатора.
Рис.4: Диаграмма эквивалентной цепи трансформатора
Рис.5 (a): Эквивалентная схема трансформатора относительно первичной стороны
Рис.5 (b): Эквивалентная схема трансформатора относительно вторичной стороны
Примерная эквивалентная схема трансформатора, относящаяся к первичной и вторичной стороне
Выведение примерных эквивалентных схем начинается со схем, показанных на рис.5. Все величины относятся к одной и той же стороне трансформатора, и идеальный трансформатор может не включаться в эквивалентную схему.
Первым шагом в процессе упрощения является перемещение ветви намагничивания шунта из середины Т-цепи либо к первичной, либо к вторичной клемме, как показано на рисунках 6 (a) и (b).